Data Structures and Algorithms Flashcards
Given a double ‘x’ and an integer ‘n’. Write a function to calculate ‘x’ raised to the power ‘n’. For example:
power (2, 5) = 32
power (3, 4) = 81
power (1.5, 3) = 3.375
power (2, -2) = 0.25
Naïve Approach : Multiply ‘x’ by ‘n’ times, this is O(n) complexity
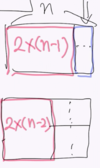
Improved Solution : Use Divide and Conquer. We divide the exponent by 2 until we reach the base case 1. This will give us logarithmic time & space complexity.
- *Case 1)** We can express 2 ^ 5 as 2 * 2^(5/2) * 2^(5/2),
- *Case 2)** if the exponent is even, 3^4 = 3^(4/2) * 3^(4/2);
const powerOfNumRecurse = function(x, n) {
if (n === 0) {
return 1;
}
if (n === 1) {
return x;
}
let temp = powerOfNumRecurse(x, Math.floor(n/2));
let result;
//check if n is even or odd
if (n % 2 === 0) {
return temp \* temp;
} else if (n % 2 === 1) {
return x \* temp \* temp;
}
};
const powerOfNumMain = function(x, n) {
let isExpNegative = false; let result;
if (n \< 0) {
isExpNegative = true;
//turn n into positive
n \*= -1;
}
let result = powerOfNumRecurse(x, n);
if (isExpNegative) {
return 1/result;
}
return result;
};
Remove Duplicates from a linked list. The linked list can be sorted, or unsorted. Give two solutions, one with O(1) memory space, and one without memory restrictions
Solution #1 : Memory Space O(1). Works for both sorted/unsorted. Use HashSet to store value of all linked lists we’ve seen so far, O(n) space and time complexity. If we see a value we’ve stored already, just skip over it.
Key : Use prev and current again, with prev initialized to null, and current at head. If it’s a duplicate value that we’ve seen before, just skip over it by connecting previous to current’s next. Otherwise, add current value to our hashSet, and just advance prev and current.
Solution #2: If the list is sorted
Since the list is sorted this means duplicates are adjacent to each other. We can do a linear scan starting from head, and only connect to next node if it’s a new value.
Key : Use prev and current again, but with prev at head, and current at head.next.
We’ll traverse through the list, and update prev’s next pointer only if current’s value is new.
Don’t forget to update prev’s next to null. Since it’ll be the tail node in our updated list.
const removeDuplicatesSorted = function(head) {
//if head is null, or linked list has length 1, return the list as is.
if (!head || !head.next) {
return head;
}
//start at second node as current to prevent null error let prev = head; let current = head.next;
while (current !== null) {
//We only do anything, EVER if current's a different value from prev.
if (current.val !== prev.val) {
prev.next = current;
prev = current;
}
//Otherwise just keep on trucking. current = current.next; }
prev.next = null;
return head;
}
Implement in-order traversal iteratively.
Question asked when stuck : how do we examine root’s left and root’s value? Answer : They’re the same. When we pop, the root we’re looking at IS the parent’s left. So all we have to do is examine the value right after we pop from the stack.
Hint : First try with a simple BST using a stack. The key to understanding this is that whenever we pop, we move up one level and we access the parent.
Then we can decide what to do with the parent(root), or the root’s right. Key : We have an inner while loop that goes deep into the left subtrees as long as the current node we’re looking at isn’t null. We need this INSIDE the outer while loop because when we go RIGHT, we have to examine the left sub-trees of that right subtree.
Solution #1: Initialize currentNode to root. We will iterate as long as currentNode exists, and our stack isn’t empty. We need an inner while loop that keeps going deeply left as long as currentNode exists, pushing to the stack each time. If currentNode is null, we simply pop from the stack, examine it. And then go right.(Set currentNode to currentNode.right);
Solution #1: using two cases(current node is null, or not). Key to understanding this is that with DFS, the currentNode we’re looking at will either be null, or not null. If it’s null, that means we can safely move up one level. So we’ll be popping from the stack. Start by initializing a stack and setting current node to root. While loop as long as stack isn’t empty or current node exists.
Case 1) node isn’t null, go left! push to stack and set node to node.left
Case 2) node is null. Move up one level. First pop the node(Moving up one level), and examine it. Then go right! set node to node.right
Given a list that represents a permutation of a list, find the next permutation in lexicographical order.
Let’s say we have 1, 3, 6, 5, 4
The next permutation in lexicographical order is 1,4,3,5,6. How did I know that?
1. I examined the number right to left looking for the first increasing sequence( 3 -> 6). I know that this is where number swaps will happen to find adjacent permutations.
Go right to left, trying to find A[i-1] <= A[i]. We are finding the first decreasing sequence(right -> left) So A[i] is 6, and A[i-1] is 3.
2. Then, we search right to left, trying to find the number that’s JUST larger than A[i-1]. This is because that’s the number that will come ‘NEXT’ in lexicographical order and replace the number A[i]. This number will exist on the right side of A[i-1].
So step 2 : Go right to left, trying to find A[j] >= A[i-1], as long as j >= i. So in here we’re trying to find the largest element that’s JUST LARGER than A[i-1]. The maximum element to the right of A[i-1]. A[j] is 4.
Step 3. Swap A[i-1] and A[j]. We swap 3 and 4.
Step 4. Since we picked out the maximum to the right of A[i-1], the sequence to the right of A[i-1] will be in decreasing order. We simply REVERSE elements from A[i] to make it increasing order.
const swap = function(list, a, b) {
let temp = list[a];
list[a] = list[b];
list[b] = temp;
}
const nextPermutation = function(nums) {
let i = nums.length-1; let j = nums.length-1;
//this loop breaks until we find nums[i-1] \<= nums[i]
while (i \> 0) {
if (nums[i-1] \<= nums[i]) {
break;
}
i--;
}
// if (i <= 0) return false; //If i === 0 this is the LAST permutation since i is the largest number
if (i > 0) {
while (j >= i) {
if (nums[j] >= nums[i-1]) {
break;
}
j–;
}
//swap only if i is greater than 0 //This means we only swap if it's not the LAST permutation, since for the last permutatio we don't want to do anything until the reversing part. swap(nums, j, i-1); }
//reset j
j = nums.length-1;
//reverse from i till end
while (i < j) {
swap(nums, i, j);
i++;
j–;
}
};
Find the Nth fibonacci number using memoization. Do it bottom-up and top-down.
TOP-DOWN
const fibonacciRecurse = function(n) {
//D[n] = D[n-1] + D[n-2];
const memo = {};
const subroutine = function(n) {
//base case
if (n \<= 1) return n;
if (memo[n]) {
return memo[n];
}
memo[n] = subroutine(n-1) + subroutine(n-2);
return memo[n];
};
subroutine(n);
return memo[n];
};
BOTTOM-UP
const fibonacciBottomUp = function(n) {
const memo = {};
memo[0] = 0;
memo[1] = 1;
for (let i = 2; i \<= n; i++) {
memo[i] = memo[i-1] + memo[i-2];
}
return memo[n];
}
Implement a Min Stack that supports getMinimum() in constant time.
Two solutions :
#1. Use an extra stack to hold the minimum. We only push to the minStack if it’s a new minimum(If it’s less than or equal to the minimum). This is because we have unique cases with duplicate values! Otherwise we don’t push. On pop(), just check if it’s a minimum we’re popping and then update the minimum as necessary.
#2. Use a tuple to store [element, currentMinimum] as our data.
On push(), update minimum if it’s a new minimum we’re pushing to stack.
Stack.prototype.push = function(elem) {
let currentMin = this.getMinimum();
//if it's a new minimum, update currentMin to elem.
if (currentMin === null || elem \< currentMin) {
currentMin = elem;
}
//store both elem, along with currentMin
this.storage.push([elem, currentMin]);
}
Stack.prototype.getMinimum = function() {
if (this.storage.length === 0) {
return null;
} else {
return this.storage[this.storage.length-1][1];
}
}
Delete a node from a BST, explain how it’ll be done.
Basic Approach : We will be using a recursive approach to handle deleting a node from BST.
We can break it down to three general cases :
Case 1) Node to delete is a leaf node. In this case all we have to do is set the node to root, and return it.
- *Case 2)** Node to delete has one child. In this case all we have to do is set the node to the other existing child, and return it.
- *Case 3)** Node has two children. This one is a bit more tricky, but we basically find the minimum in the right subtree and copy the value to the node. Then we delete the minimum in the rightsubtree(Use our recursive function).
An important detail in this implementation is to return the root(node) every time so that the properly adjusted nodes are returned up to recursion and we can set the pointers accordingly.
const findMin = function(root) {
if (!root) return null;
while (root.left) {
root = root.left;
}
return root;
};
const deleteNode = function(root, key) {
if (!root) return root;
if (root.val \< key) {
root.right = deleteNode(root.right, key);
} else if (root.val \> key) {
root.left = deleteNode(root.left, key);
} else if (root.val === key) {
//Case 1 : leaf node
if (!root.left && !root.right) {
root = null;
}
else if (!root.left) {
root = root.right;
}
else if (!root.right) {
root = root.left;
}
else {
let minInRight = findMin(root.right);
//copy minInRight's value into root
root.val = minInRight.val;
root.right = deleteNode(root.right, minInRight.val);
}
}
console.log(‘root :’, root);
return root;
};
Find an inorder successor in a BST.
Naive Solution : Create a list of all the nodes in in-order traversal, and do a linear scan to find the successor. O(n) time, where n is the number of nodes.
Optimized Solution : If you look at finding in-order successor, there’s two cases :
Case 1) Current node has a rightChild. Then our successor is the minimum in the rightChild. Or the leftmost node in the rightChild.
Case 2) Current node has no rightChild. In this case, this is the confusing one - we have to pop back to the parent. There are two cases, if this node is a leftChild or a rightChild of the parent. If it’s a leftChild, we simply return the parent since it’s the successor. If it’s the rightChild, we have to find the parent’s parent(Since the immediate parent would have already been visited). So we have to go to the closest ancestor for which our node would be in its left subtree. Understand this, and the problem is easy.
KEY : We need to implement a findMin() function, the iterative version using a while loop is much cleaner.
Basic Approach : Every time we go LEFT to find our targetNode, just remember the potential successor since it’ll become the parent.
const findMin = function(root) {
if (!root) return null;
while (root.left) {
root = root.left;
}
return root;
};
const inorderSuccessor = function(root, p, successor) {
if (!root) return null;
successor = successor || null;
//going left
if (root.val \> p.val) {
return inorderSuccessor(root.left, p, root);
}
//going right
else if (root.val \< p.val) {
return inorderSuccessor(root.right, p, successor);
}
//we've found our node
else if (root.val === p.val) {
//two cases
if (root.right) {
return findMin(root.right);
} else if (root.right === null) {
//return successor
return successor;
}
}
};
Implement a Queue using stacks. Optimize for push() and for pop() in return.
Solution #1., push() is constant, and pop() is O(n).
Use inStack and outStack. Always push to inStack. For pop(), pop from outStack if outStack isn’t empty. If it is empty, we need to pop everything from inStack and push to outStack, and pop the top of outStack.
Since the runtime of outStack depends on how many elements there are on outStack at that given moment(Can be constant if there are items), the more expensive a O(n) dequeue is, the more O(1) it WINS us in the future.
Solution #2. If we optimized for pop() instead.
For pop(), we’ll just pop from stack1.
For push(), we’ll take out everything from stack1, put it into stack 2. Then we push the newest item to stack1. Then we’ll pop everything from stack2 back into stack1. So essentially we’re doing two exchanges between stack1 and stack2, except in the middle we push the newest item in stack1, because this puts the newest item at the back of the queue. In a way we’re using stack2 as a temporary holder, and putting the newest item at the back of the queue to preserve order.
Given a BST class, implement a delete method to delete a node from a BST.
The important thing with deleting a node from BST’s is that we need need access to the parent(Since we have to re-set the parent’s links to its left/right). To achieve this, we will use recursion, and return the current tree(‘root’) at every execution so that when it returns up, the parent has access to the child.
Also, instead of using ‘this’ we will pass in an additional argument, ‘root’ because we won’t be able to re-set the ‘this’ context.
After this, we can break down deletion into three different cases :
First, we have to find our node by going left/right while comparing our root data against the input value. Use recursion here as well to re-adjust the children links.
1) Leaf node(No children)
2) One child
3) Two children
Since we’re returning the root at the end, in each case we simply want to modify the root value. Case 3 is the only tricky one, since we want to first find the minimum in the right-subtree, copy over its data into the root, and then DELETE that duplicate node in the right subtree. Essentially we have a smaller problem of deleting that minimum node in the right subtree.
//Pass the parent as an argument!
*BinarySearchTree.prototype.delete = function(val, root) {
//we will have to re-set 'this'(which isn't possible), so we will pass in an additional parameter called root that will be initialized to 'this'
root = root || this;*
if (!root) return null;
*//Go left
if (root.data \> val) {
root.leftChild = root.delete(val, root.leftChild);*
*//Go right
} else if (root.data \< val) {
root.rightChild = root.delete(val, root.rightChild);
} else {
//We've found our node, need to delete it*
*//Caes 1 : Leaf node
if (root.leftChild === null && root.rightChild === null) {
root = null;
} else if (root.leftChild === null) {
//Case 2 : Only rightChild or Only leftChild
root = root.rightChild;
} else if (root.rightChild === null) {
root = root.leftChild;
} else {
//Case 3 : Two children*
*//Find minimum in rightSubtree
let minInRightSubTree = root.rightChild.findMin();
console.log("minInRightSubTree :", minInRightSubTree);
//Copy this data into root!
root.data = minInRightSubTree.data;*
//now there is a duplicate node in RightSubtree, delete it(We’re calling it FROM the reference of the right subtree.)
root.rightChild = root.delete(minInRightSubTree.data, root.rightChild);
}
}
*//Don't forget to return root return root; };*
You’re given N pieces of bread. If the # of profit that you can make on selling i pieces of bread is P[i], find the maximum profit you can make from selling N piece of bread. As input, first you’re given the number of pieces of bread you can sell. The second input is P[i] from P[1] to P[n]. EX : For 4 pieces of bread, P[1] = 1 P[2] = 5 P[3] = 6 P[4] = 7 Since for 4 pieces, you can sell 2 pieces twice, 5 * 2 = 10.
We start by defining D[n] as the maximum profit I can make by selling n pieces of bread. Now we can clarify the problem as : Selling x + y + z = n So we sell x pieces of bread to one person, y pieces of bread to another, z pieces to another to total n pieces of bread. Note how many pieces we can sell to this last person. We can sell anywhere between 1 pieces to the whole batch, N pieces. If the last ‘batch’ we sell bread to is one person, D[n] = D[n-1] + P[1] because P[1] is the profit we can make by selling one piece. If it’s two people, D[n] = D[n-2] + P[2] … D[n] = D[0] + P[n] Then, we can express D[n] as D[n] = Max(D[n-i] + P[i]) where i is the # of people we sell bread to. 1 <= i <= n.
const sellFishBread = function(n, profitList) {
const memo = {};
memo[0] = 0;
memo[1] = profitList[0];
//i goes from 1 to n, denoting the total # of fishbread we sell
for (let i = 1; i \<= n; i++) {
//j denotes the number of fishbread we sell to the last person
for (let j = 1; j \<= i; j++) {
if (!memo[i]) {
memo[i] = memo[i-j] + profitList[j-1];
}
memo[i] = Math.max(memo[i], memo[i-j] + profitList[j-1]);
}
}
return memo[n];
};
Find maximum depth of a tree
Key Point : Think of the smallest case. We want to find the maximum depths of the left subtree and the right subtree. However, since we’re going down one level, we add 1 to whatever the maximum of those two values are.
Simple Recursive Solution :
const maxDepth = function(root) {
if (!root) return 0;
return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
};
/*
Given a directed graph, design an algorithm to find out whether there is a route between two nodes.
*/
BFS/DFS.
With BFS : Can find shortest path bewteen the two nodes.
We use a queue, and a visited set to keep track of nodes visited. At each point if the node we’re examining next is the destination node, we return true.
When implementing DFS, be careful about return values from the recursive functions. We’re returning a boolean, so we can’t return the recursive calls immediately. Spawn off the recursive calls(Don’t return them), if any of them return true, then return true!
const routeDFS = function(sourceNode, destinationNode) {
const visited = new Set();
let current;
let neighbors;
const dfsRecurse = function(node) {
if (node === destinationNode) {
return true;
}
visited.add(node);
neighbors = node.getNeighbors();
for (let nextNeighbor in neighbors) {
if (!visited.has(nextNeighbor)) {
//if any of the recursive calls return true, return true immediately.
if (dfsRecurse(nextNeighbor)) {
return true;
}
}
}
return false;
};
return dfsRecurse(sourceNode); };
Given two non-empty binary trees s and t, check whether tree t has exactly the same structure and node values with a subtree of s. A subtree of s is a tree consists of a node in s and all of this node’s descendants. The tree s could also be considered as a subtree of itself.
Important thing to note here is that in-order traversal won’t work. The reason is, because in a BST, in-order traversal will always print out the nodes in the same order even if the structures are different(Just work through a simple example like [1,0,2] and [null, 0, 1, 2].
So we have to use pre-order traversal, where the order is determined by the traversal itself. We just have to remember to pad the null nodes with ‘null’, and create string representations of each traversal. Afterwards, we check if one is a substring of another.
The runtime of this is O(m * n + m^2 + n^2). This is because we spend linear time with each traversal, and string concatenation takes linear time(Which makes it quadratic), and indexOf takes O(m*n). Space complexity is O(m + n), for each of the strings.
Another approach that’s easier, is simply traverse the first tree until we find a node that’s equal to the second root. Then we recursively call an isEqual helper(Easy to implement). This seems like O(m*n), because each time a node in TreeOne matches TreeTwo, we call an isEqual helper that essentially traverses all nodes in TreeTwo. However, we don’t actually call isEqual on all of TreeTwo, we call it k times, where k is the # of occurrences of TreeTwo’s root in TreeOne.
const isEqual = (treeOne, treeTwo) =\> {
if (treeOne === null && treeTwo === null) return true;
if (treeOne === null || treeTwo === null) return false;
if (treeOne.val !== treeTwo.val) return false;
//they both have values.
return (
isEqual(treeOne.left, treeTwo.left) && isEqual(treeOne.right, treeTwo.right)
);
};
var isSubtree = function(s, t) {
if (s === null) return false; //if the larger tree is null and we havent found the subtree return false.
if (isEqual(s, t)) return true; return isSubtree(s.left, t) || isSubtree(s.right, t); };
Solve the classic Tower of Hanoi Problem, where you’re given n disks in decreasing size(bottom->top) and you have to move them from Peg A to Peg C, using an auxiliary Peg B in the middle.
We start by first considering cases for 1 disk, 2 disks, and 3 disks.
If we only have one disk, we simply move from A -> C using B.
If we have two disks, we first move the smallest disk A -> B. Then move the larger disk from A -> C, then move the smaller disk from B -> C.
Now let’s look at three disks. After going through all the steps, we can see that we can express the three disk problem as :
1). Move 2 disks from A -> B.
2) Move 1 disk(Largest disk) from A -> C.
3) Move 2 disks from B -> C.
No matter the number of disks, every problem can be expressed as such, since we know that the largest disk has to be on the bottom of C. Then we move the rest of the disks to C.
So we can express the recursive algorithm as such :
1). Move n-1 disks from A -> B.
2) Move 1 disk(Largest disk) from A -> C.
3) Move n-1 disks from B -> C.
const towerOfHanoi = function(n, start, mid, end) {
if (n === 1) {
console.log(start, ‘—->’, end);
return;
} else {
towerOfHanoi(n-1, start, end, mid);
towerOfHanoi(1, start, mid, end);
towerOfHanoi(n-1, mid, start, end);
}
};
Zip a linked list from two ends
1->2->3->4->5->6
Output : 1->6->2->5->3->4
Straightforward, Clean Approach :
Split the linked list in the middle, then reverse the second half. Then merge the two lists together, taking one node from each list one at a time.
Recursive approach, slightly more complicated :
Use recursion to access the elements from end to back. This is slightly more complicated because : We need to use a flag to stop the recursion from doing more work after reaching the middle of the list, and also because we have to handle odd # and even # cases.
const zip = function(pList) {
let front = pList;
let temp = pList;
let flag = true;
const recurse = function(back) {
if (back === null) {
return;
}
//go to the tail recurse(back.next);
//
if (front.next === back || front === back && flag) {
back.next = null;
flag = false;
}
if (flag) {
//save the original next first.
temp = front.next;
front.next = back;
back.next = temp;
front = temp;
}
};
recurse(front);
return pList;
};
Implement a stack using queue(s). Implement push, pop, top, isEmpty and discuss their runtimes.
Question to ask the interviewer : Do we want to optimize for push() or for pop() ? Since we’re using two queues, we can get constant time for one of them, but linear time for the other.
KEY : Since queues, with enqueue() and dequeue() preserve the original order, we can’t just transfer them back and forth between each other. All we care about is the last item, that’s the only order we have to be able to access. So we’ll use one of the queues to ‘remember’ this last item added. We use one of the empty queues to ‘hold’ the last item added, and dequeue all other elements to that queue. This last item then becomes the first item in the queue. It ‘cheats’ its way back into the first of the line.
Also to avoid taking items out and putting them back into another second time, we SWAP references between the two queues when we’re done.
Solution #1., Optimizing for push() O(1), and pop() O(n).
For push, just push to queue1 always.
For pop(), the interesting one, we dequeue everything from queue1 and put them in queue2, except for the last item. Since we’ve dequeued everything except for the last one, we know this is the last item in the queue. We return this item. We also swap queue1 and queue2’s references.
Solution #2. push() O(n), pop() O(1).
This one is a little bit more tricky, but when we push we’ll be using queue2 to make the last item added cheat its way to the front of the queue to be dequeued first(That way it’s the top item).
For push(), first enqueue to queue1 if it’s empty. If it’s NOT empty, enqueue to queue2, and here’s the key part - dequeue everything from queue1 and enqueue to queue2. Since we’ve enqueued to queue2 the newest item BEFORE the emptying out of queue1, the newest item is in FRONT of the queue.
Then swap queue1 and queue2, so that for pop we’re always dequeuing from queue1.
This is why for pop(), we simply pop from queue1.
Implement post-order traversal iteratively. This is trickier than the other DFS traversals.
With post-order we’re looking at
The way we will solve this is by using another variable called visited to keep track of previously visited node. This will prevent us from re-visiting the <ROOT>when we go left, then right, then back to>.
So what we will do is go all the way to the left first.
Then we will peek the top of the stack. We check if it has a right subtree. If it has a right subtree AND the right subtree HASN’T been visited yet, this means we’ve visited so it’s time to visit the node. So we set currentNode to the rightChild of top(top of stack).
Otherwise, this means this is a leftChild so we can safely pop from our stack and visit it. We make sure to set the visited variable to this node.
We then set currentNode to null, so we can move up one level.
So we do solve this the same way we solve the other two, dividing it into two large cases.
Case 1) current node exists We have to keep going left, so push current node to stack, and set node = node.left. Simple.
Case 2) current node is null. This is the tricky part. First we peek the top of the stack’s rightChild(“temp”).
Subcase 1) If temp doesn’t have a rightChild, this means temp is a leaf node <LEFT>. so we’re ready to visit it. Pop temp from stack and examine it.
Then we need to check if temp was a rightChild of current stack’s top. If it WAS a rightChild of top, we pop node from stack and visit the node. Since that means we’re going <RIGHT> ->.
Subcase 2) Right child exists, which means we have to look at the right sub-tree first. Go right by setting current = temp. We’re essentially going up one level(to parent), then going to parent’s right subtree.
Find all permutations of a string. String may include duplicates.
If we didn’t have duplicates, we could use the swapping method to fix one character, and swap the rest one by one and using a backtracking solution to solve it. However, since we have to handle duplicates, we will use extra memory, a map to keep track of remaining character count.
Basic Approach : What we’ll do is keep track of remaining count for each character. Then, we will iterate over our list of unique characters, left-right, looking for the next available character(This means remaining count is NOT 0). If we find it, we’ll push the chosen character into the list. We make sure to update the character count at every step. We’ll use index, or level to keep track of the depth of the recursion and reach a base case when our level equals the length of our input.
const permuteUnique = function(nums) {
//generate a map with element : count
const countMap = {};
nums.forEach(function(elem) {
if (!countMap[elem]) {
countMap[elem] = 1;
} else {
countMap[elem] += 1;
}
});
const elements = []; const count = []; let index = 0;
for (let elem in countMap) {
elements.push(elem);
count.push(countMap[elem]);
}
const result = [];
//Recursive algorithm, we go from left to right looking for the next available character(IF remaining count is not 0). Then we push the character into result list. We used this character so we update the characterCount. We use level to keep track of the depth of the recursion.
const generate = function(currentLevel, generated) {
if (currentLevel === nums.length) {
result.push(generated.slice());
return;
}
//look for the next available character. We iterate only up to the number of distinct elements' length...THIS IS KEY.
for (let i = 0; i \< elements.length; i++) {
let currentChar = elements[i];
if (count[i] === 0) {
continue;
}
//add current character to generated
generated[currentLevel] = currentChar;
//decrement characterCount
count[i] -= 1;
//Enter next recursive call
generate(currentLevel+1, generated);
//Put character Count back
count[i] += 1;
}
};
generate(0, []);
return result;
};
Detect if a linked list has a cycle. Then also, find the length of the cycle, and the beginning of the cycle.
- *Solution using a hash table :**
- As we traverse, we store **something that’s unique about each node**, whether it be data(if data is guaranteed to be unique), or references to the node.
- These references are **logical**, and not **physical addresses**, because if the nodes are spread acrosss multiple servers, you may think they’re the same even though they’re different.
- Using hash table to see if “Have I seen this node before?”
- *Another solution:**
- “Coloring Technique” : As you go, color nodes you’ve seen before previously
- Need to extend linked list data structure.
- *Solution using fastRunner/slowRunner**
- If the two runners are going the same direction, as long as one runner is faster than the other, they will meet.
- *Common Errors**
- checking if
fast === slowin the beginning of the while loop, won’t work for linked lists that **only have one length**. - *Finding the length of the cycle**
- Once we reach our anchor, where
fast === slow, start a counter from 0, and when we reach the anchor again we’ll have the length of the cycle.
-
Finding the start of cycle.
- Essentially we’re using the same logic for the problem of finding the **nth node from the end**.
Given an array of integers, rotate the array by N elements.
The algorithm for this is straightforward : 1. Reverse the array. 2. Reverse indices from 0 ~ n-1. 3. Reverse indices n ~ length-1 Example : [0,1,2,3,4,5] rotated by 3 is [3,4,5,0,1,2]. When you reverse the original list you get [5,4,3,2,1,0]. Then reversing from index 0 ~ 2 you get [3,4,5, 2,1,0]. Then we reverse from 3 to 5. Which results in [3,4,5,0,1,2]. Simple reversing using index function : const reverseArray = function(arr, start, end) { while (start < end) { //swapping let temp = arr[start]; arr[start] = arr[end]; arr[end] = temp; start++; end–; } };
Given a string s, partition s such that every substring of the partition is a palindrome.
Return all possible palindrome partitioning of s.
For example, given s = “aab”,
Return
[
[“aa”,”b”],
[“a”,”a”,”b”]
]
Approach : While this might seem like a difficult problem, it’s just a backtracking solution. Follow the general pattern for solving backtracking problems.
KEY : The only things we have to worry about are :
- Creating substrings
- Checking if the substring created is a palindrome(Use helper function).
- It’s helpful if the palindromeChecker function takes two indices, start and end.
const isPalindrome = function(string, low, high) {
while (low \< high) {
if (string[low++] !== string[high--]) return false;
}
return true;
}
var partition = function(s) {
const result = [];
const recurse = function(startIndex, soFar) {
if (startIndex === s.length) {
result.push(soFar.slice());
}
for (let i = startIndex; i < s.length; i++) {
//only push to list if current substring(startIndex ~ i) a palindrome
if (isPalindrome(s, startIndex, i)) {
let currentSubstr = s.substring(startIndex, i+1);
console.log(‘currentSubstr :’, currentSubstr);
soFar.push(currentSubstr);
recurse(i+1, soFar);
soFar.pop();
}
}
};
recurse(0, []);
return result;
};
Implement pre-order traversal iteratively. Explain how it should be done.
Think about the smallest case!!
With pre-order we want to visit the root first, then its left chilren, then its right children.
The important idea here is to use a stack to hold the nodes, as well as the result array to store the results as we traverse pre-order style.
KEY : Since we want to visit root first, we push root values to result AS we traverse down to the left/right. There is no need to push as we pop back up!!! Meaning we only need to push ONCE.
Solution #1 : Start by pushing rootNode into stack. Then all we have to do is pop it, and if the node’s value exists, 1) examine it 2) push to stack node’s right 3) push to stack node’s left ***Note how we push right node first, even though in pre-order it’s . This is because when we pop from the stack, with LIFO leftNode will be popped first.
Solution #2 : Hint : Again, think about the simplest case… Key Point : With pre-order we need to store root’s value AS we traverse down - We use stack to keep track of our root nodes as we traverse down.
As long as node exists, we examine the value first(Since pre-order is root first). We store it in result
Then we push to the stack. We need to push every node we look at to the stack since it’s the only way we’ll be able to move back up(Think recursion).
If node is null, that means we can move up, so we pop from stack(we look at the parent). Then we examine the parent’s right sub-tree.(we’ve already looked at root, so no need to do any pushing here)
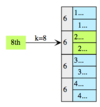
Swap kth node from the beginning, with kth node from the end.
Test cases:
swapNodes(list({11, 4, 6, 7, 1, -99, 0, 2}), 2) ⇒ | 11 | -> | 0 | -> | 6 | -> | 7 | -> | 1 | -> | -99 | -> | 4 | -> | 2 | -> Nil
Approach : We can break the problem down into two phases :
- First we have to find the kth node from the beginning, and kth node from the end.
- We have to swap them.
To swap nodes in a linked list, we need access to the previous elements of the nodes. We will first connect the previous pointers to each other(nodes), then we will connect the nodes’ next pointers to each other’s nexts.
We account for the cases where prevOne or prevTwo might be null, in which we have to reset the heads.
Don’t forget to return the new head in the swapping helper.
const swapper = function(head, prevOne, nodeOne, prevTwo, nodeTwo) {
console.log(‘head :’, head);
console.log(‘prevOne :’, prevOne);
console.log(‘nodeOne :’, nodeOne);
console.log(‘prevTwo :’, prevTwo);
console.log(‘nodeTwo :’, nodeTwo);
if (!nodeOne || !nodeTwo) return;
//if prevOne is null, this means we're swapping the head node.
if (!prevOne) {
head = nodeTwo;
} else {
prevOne.next = nodeTwo;
}
// k \> n-k
if (!prevTwo) {
head = nodeOne;
} else {
prevTwo.next = nodeOne;
}
//swap! let temp = nodeOne.next; nodeOne.next = nodeTwo.next; nodeTwo.next = temp;
return head;
};
function swapNodes(pList, iK) {
if (!pList || iK <= 0) return;
let prevOne = null; let prevTwo = null; let temp = pList; let nodeOne = pList; let nodeTwo = pList;
//find the kth node from beginning first.
while (iK \> 1 && temp) {
iK--;
prevOne = temp;
temp = temp.next;
}
//at this point, nodeOne is at kth node from beginning. nodeOne = temp;
//now we move nodeTwo(head) and temp together until temp reaches the end
while (temp && temp.next) {
prevTwo = nodeTwo;
nodeTwo = nodeTwo.next;
temp = temp.next;
}
return swapper(pList, prevOne, nodeOne, prevTwo, nodeTwo); }
Given an integer n, and k, find the kth permutation in
Sort a singly linked list using merge sort, ascending order.
ex) 1->5->6->3->4 // 1->3->4->5->6
Merge sort has three steps you need to know.
- Dividing the list into two.
- Merging the two lists together
- Recursive structure(Divide & Conquer). The way this is done is you call the function recursively on the split halves, firstHalf and secondHalf, and return the merged list each time.
Dividing potion : We use slow pointer, fast pointer method to find the middle of the list. But we initialize slow to head, and fast to head.next, so that when fast reaches the end of the list, slow is at the node previous to the midpoint. All we have to do is initialize slow.next to be returned, and then split the list into two by setting slow.next = null.
Merge step : A lot of details to be careful of here. First, handle the edge cases where either / both heads are null.
Then, find the newHead by comparing the values of headA and headB. This is the returned value, since we need to return the head of the newly merged(sorted) list. We will need to initialize another variable, sortedCurrentNode to advance through the sorted list.
Then, we iterate through headA and headB, appending to sortedCurrentNode each time.
Once we’re done, we can check if there are any nodes remaining in either headA, headB, and simply attach it to the end of sortedCurrentNode.
const splitIntoTwo = function(head) {
//if list is length 0 or 1 just return the head
if (!head || !head.next) return head;
let slow = head; let fast = head.next;
while (fast && fast.next) {
slow = slow.next;
fast = fast.next.next;
}
//at this point, slow will be at the midpoint. save slow’s next(Which is the secondHalf’s head) to a variable, and split the list by setting it to null afterwards
let secondHead = slow.next; slow.next = null;
return {firstHalf : head, secondHalf : secondHead};
};
const merge = function(l1, l2) {
//first if either head is null, return the other
if (!l1) return l2;
if (!l2) return l1;
//first find the 'new' head by comparing l1's value and l2's value
//\*\*\*DONT forget to move l1 and l2 after setting head.
let newHead = null;
if (l1.val \<= l2.val) {
newHead = l1;
l1 = l1.next;
} else {
newHead = l2;
l2 = l2.next;
}
//Need to save newHead HERE, to be returned later. let sortedNodeCurrent = newHead;
//iterate through l1 and l2, appending the larger node to newHead
while (l1 && l2) {
if (l1.val \<= l2.val) {
sortedNodeCurrent.next = l1;
l1 = l1.next;
} else {
sortedNodeCurrent.next = l2;
l2 = l2.next;
}
sortedNodeCurrent = sortedNodeCurrent.next;
}
//Edge cases! If either list is left over, just add it to the end of newHead
if (l1) {
sortedNodeCurrent.next = l1;
} else if (l2) {
sortedNodeCurrent.next = l2;
}
return newHead;
};
const mergeSortedLinkedList = function(head) {
if (!head || !head.next) {
return head;
}
let splitHeads = splitIntoTwo(head); let firstHead = mergeSortedLinkedList(splitHeads.firstHalf); let secondHead = mergeSortedLinkedList(splitHeads.secondHalf);
let merged = merge(firstHead, secondHead); return merged; };
Serialize/Deserialize a BST. What’s the definition of serializing something?
Serialize : Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
To serialize a BST, we will use an array as a stream - and in the stream we will store all the nodes using DFS, pre-order. We will use a MARKER(*) to denote null nodes. We use the * because using -1 means we can’t use -1 value BST Nodes, and using Number.MAX_VALUE sometimes results in stack overflow.
Serialize Approach : To serialize tree, initialize an array(will be stringified and returned in the end) as our stream, and initialize MARKER(*). Since we’re going pre-order, we handle the base case first, where if current node is null(Then we’ll push MARKER into stream). Otherwise, store current node’s value in stream, and recursively call subroutine on current node’s left, followed by right.
De-serialize Approach : We will first split the string to make it an array. In our subroutine, we wrap everything inside a try-catch block, since reading from our file(input) may result in an error. We shift the first element in our stream, and examine it - if it’s our MARKER, return null. Otherwise, we create a new BSTNode with the value. Then we assign node.left to subroutine(stream), and node.right to subroutine. We don’t forget to return the node after the recursive calls.
Given a sorted, rotated array without duplicates, find out how many times it was rotated
Naive solution : Use linear search to find minimum element. Index of minimum gives us the # of rotations(Think about it). We can use a modified version of binary search to cut this down into O(log N) time. Key Point : What unique property does the minimum ‘pivot’ have? Also, what allows us to use binary search? The fact that 1/2 of the array will ALWAYS be sorted at a given time. However, if mid isn’t pivot, we know that if left half of the array is sorted, pivot cannot exist in the left half. ex : [3,4,5,6,0,1,2], mid is 6. Mid isn’t pivot, so we look at left half. It’s sorted, which means pivot can’t exist in the left half. So we have to go right. So this allow us to discard 1/2 of the array every single time. ————————————————————– The algorithm : Case 1 : Array[low] <= Array[high] : This means the array is already sorted, return low(Thats the minimum) Case 2 : Check if array[mid] is a ‘pivot’. If so, return mid. Pivot’s unique property is that its previous and next elements are both greater than it. **When checking next and previous, make sure to use modulo function to wrap around the list. previous = (mid -1 + N) % N; Case 3 : Right half is sorted, so search the left half Case 4 : Left half is sorted, search right half ——————————————————————– Finding prev and next from mid(we have to make sure they wrap around the array) : next = (mid+1) % arr.length prev = (mid-1 + arr.length) % arr.length
Given an integer N, find the total number of ways to express it in sums of 1, 2, or 3.
Ex) If we are given 4,
1 + 1 + 1 + 1
1 + 1 + 2
1 + 2 + 1
2 + 1 + 1
2 + 2
1 + 3
3 + 1
In total, there are seven different ways to express 4 in sums of 1, 2, or 3.
So we start by defining D[n], which is the total # of ways a number can be expressed using 1, 2, or 3. If we express N in sums of different numbers, x + y + …. + z = N This last number z can be 1, 2, or 3. 1) x + y + …. + 1 = N N-1 + 1 = N So the sum of all the numbers before the last number is N-1. Therefore, the # of different ways to generate N-1 becomes D[n-1].
Since we need to consider all three possibilities, D[n] = D[n-1] + D[n-2] + D[n-3].
Just consider 4 as an example.
BOTTOM-UP:
const sumOfOneTwoThree = function(n) {
const memo = {};
memo[1] = 1;
memo[2] = 2;
memo[3] = 4;
for (let i = 4; i\<= n; i++) {
memo[i] = memo[i-1] + memo[i-2] + memo[i-3];
}
return memo[n];
};
Given a singly linked list and the head of a singly linked list, return Nth from last node
/*
Approach 1 : Since we don’t want to end up doing two passes to find the length of the list, we set up two pointers, we can think of them like a stick, but with length N. Once the end of the stick reaches the tail(null), the start pointer will be the node we want.
First clarify with the interviewer whether if n===1, it’s the TAIL node(last node), or first node from last(second to last node)
KEY : Need to handle two edge cases :
- When n is negative or head doesn’t exist
- N is out of bounds, it’s greater than the length of the linked list. For #2, just decrement N by 1 at each point when moving the end pointer. Then check if N is equal to 0. If it’s not, then we know it’s out of bounds!
*/
const getNthFromLast = function(head, n) {
//if n is less than 1 or head is null, return null
if (n \< 1 || head === null) return null;
let start = head; let end = head;
//move end to the right, as long as
while (end && n \> 0) {
end = end.next;
n-=1;
}
//at this point, if n is not 0 this means N is greater than
//the length of the list.
if (n !== 0) {
return null;
}
//stop when end node is the tail node(its next is null)
while (end !== null) {
start = start.next;
end = end.next;
}
return start;
};
Find the total # of ways to fill up a 2*N rectangle with 1x2, 2x1 tiles.
Drawing it out will seriously help.
Start by building up from smallest cases, from 0 ~ 3.
If we draw out a rectangle, we can see that we have two cases, where the edge of the rectangle can be filled with ONE 1x2, or with two 2x1 blocks stacked horizontally.
So D[n] can be divided into two cases :
1) D[n-1] where the width is (n-1) and height is 2. D[n-1] = 2 * n-1
2) D[n-1] where the width is (n-2) and height is 2. D[n-2] = 2 * n-2 So we add the 1) and 2) to get D[n]. D[n] = D[n-1] + D[n-2].
Given a collection of numbers that might contain duplicates, return all possible unique permutations.
For example,
[1,1,2] have the following unique permutations:
[[1,1,2], [1,2,1], [2,1,1] ]
We can use the same algorithm for generating permutations, except we need a way to somehow handle duplicates. Using storage systems like map, sets WONT WORK since they can’t handle two completely different objects. So using our algorithm of in-place swaps is overkill here, since the duplicate part is confusing as fuark.
INSTEAD, what we will do is use a map to keep track of each element and its count. We will then go left to right from a list of distinct elements, looking for the next available element. The next available element is one that doesn’t have a count of 0. THE PART THAT GOT ME CONFUSED WAS I was trying to iterate over our original input(That has duplicates) and choosing from duplicates. THIS DOESNT WORK SINCE we have no way of handling duplicate characters. Instead, we only select a character from DISTINCT ELEMENTS that we know we haven’t used yet. So we transform our map to use two additional lists, elements and count. So these arrays are in the order of elements to their counts.
In the recursive algorithm, we do :
- keep track of current level. This is used to add to our result list(running total of permutation generated so far).
- when we pick a character, we make sure to decrement its count. Once we’re done with a recursive call, we make sure to put it back in its original state.
const permuteUnique = function(nums) {
//generate a map with element : count
const countMap = {};
nums.forEach(function(elem) {
if (!countMap[elem]) {
countMap[elem] = 1;
} else {
countMap[elem] += 1;
}
});
const elements = []; const count = []; let index = 0;
for (let elem in countMap) {
elements.push(Number(elem));
count.push(countMap[elem]);
}
const result = [];
//Recursive algorithm, we go from left to right looking for the next available character(IF remaining count is not 0). Then we push the character into result list. We used this character so we update the characterCount. We use level to keep track of the depth of the recursion.
const generate = function(currentLevel, generated) {
if (currentLevel === nums.length) {
result.push(generated.slice());
return;
}
//look for the next available character. We iterate only up to the number of distinct elements' length...THIS IS KEY.
for (let i = 0; i \< elements.length; i++) {
let currentChar = elements[i];
if (count[i] === 0) {
continue;
}
//add current character to generated
generated[currentLevel] = currentChar;
//decrement characterCount
count[i] -= 1;
//Enter next recursive call
generate(currentLevel+1, generated);
//Put character Count back
count[i] += 1;
}
};
generate(0, []);
return result;
};
Given a set of n elements find their kth permutation.
Naive Approach : Generate all permutations in lexicographical order, and using a counter select the kth one. This will require O(N!) Time Complexity.
Instead, we can take advantage of recursion to reduce it to a linear solution
Basic Approach : Let’s say we have an input of [1,2,3]. We know that if there are 2! permutations that start with 1 fixed. And also 2! with 2 fixed, and 2! with 3 fixed. So we can envision blocks of size (n-1)! permutations for each starting letter. What we can do is, we can use k to find which block our permutation lies in, which lets us find out what the next letter in the permutation is. We use a recursive algorithm, and for the next recursive call we simply take out the element we just used from the input list.
KEY : A couple things to watch out for here :
1. Finding the block size at each call. This is easy, just do (n-1)!
2. Selecting the index of the block that the permutation is in. In other words, finding out what the next letter is by finding the right index. This is done by subtracting k-1 and dividing it by the block size. The reason we subtract k by 1 is because, for example, if k = 12, and each block size is 3! = 6, we know we need to select from the second block(index 1). If we simply do k / blockSize = 12 / 6 = 2. We’d end up selecting the second block. You can also find the index by BaekJoon’s method of subtracting k by blockSize every time until we reach a negative number.
3. For the next function call, we reset k by computing k = k - (blockSize * selectedIndex). And we also slice out the element at currentIndex from the input list.
const factorial = function(n) {
const memo = {};
memo[0] = 1;
memo[1] = 1;
for (let i = 2; i \<= n; i++) {
memo[i] = i \* memo[i-1];
}
return memo[n];
};
const findKthPermutation = function(n, k) {
let result = ""; const list = [];
for (let i = 1; i \<= n; i++) {
list.push(i);
}
const generate = function(k, input) {
if (input.length === 0 || !k) {
return;
}
const blockSize = factorial(input.length-1); // 3!
//Get the index of the block that the permutation is in let selectedIndex = Math.floor((k-1) / blockSize); //selects block
result+= input[selectedIndex];
//splice out currentIndex element from input input.splice(selectedIndex, 1);
//reset k by subtracting it from the # of (blocks \* index) k = k - (blockSize \* selectedIndex);
generate(k, input);
};
generate(k, list);
return result;
};
