Data Analysis Flashcards
(18 cards)
When a set of data has suspect outliers, which is the (1) preferred measure of central tendency and of (2) of variability?
Median and Interquartile range
The mean, standard deviation and range are all affected by outliers.
Is there an implicit assumption is that there are more than four data points?
Using the most commonly accepted definition of outliers, a set has five outliers. If every value of the set of outliers is increased by 20%, how many outliers will there be?
5
(Ie, no change since the procedure increareases Q1, Q3, IQR, Q1 - 1.5(IQR) and Q3+1.5(IQR) by the same amount.
Correlation
Which of the following is true?
A. When r=0, there is no relationship between the variables.
B. When r=0.2, 20% of the variables are closely related.
C. When r=1, there is a perfect cause-and-effect relationship between the variables.
D. A correlation close to 1 means that a linear model will give the best fit to the data.
E. All the above statements are false.
(E) All the statements are false.
(A) is false because correlation measures only linearity; a nonlinear relationship can yield a r of 0.
(C) is false because correlation shows association, not cause and effect.
(D) is false because curved data can have correlation close to 1.
Correlation and Causation
A study finds that r=1 relating job satisfaction to salary. Which of the following is a valid conclusion?
(A) High salary causes high job satisfaction.
(B) Low salary causes low job satisfaction.
(C) There is a 100% cause-and-effect relationship between salary and job satisfaction.
(D) There is a very strong association between salary and job satisfaction.
(E) None of the above are proper conclusions.
(D)
Histograms
Which of the following is true?
(A) Two students with the same data set can produce different histograms.
(B) Displaying outliers is less problematic when using histograms than with stemplots.
(C) Histograms are more widely used than stemplots or dotplots because histograms display the value of individual observations.
(D) Unlike other graphs, histogram axes do not need to be labeled.
(E) A histogram of a categorical variable can pinpoint clusters and gaps.
(A)
(B) is false because displaying outliers is more problematic with histograms because of dependence on bin widths.
C: Histograms do not show individual observations.
D: All graphs need to be labeled
Histograms
Why can histograms produced by different workers from the same dataset look different?
The choice of interval width and therefore the number of bins affects the appearance.
Correlation
Let r=0.28. If 0.17 is added to all the values of the x-variable and every value of the y-variable is doubled, and the two variables are interchanged, what will be the new value of r ?
0.28
Correlation is not changed by the above changes.
Correlation and Regression line
Which of the following is incorrect?
(A) The correlation and the slope of the regression line always have the same sign.
(B) A correlation of -0.32 and a correlation of +.32 show the same degree of clustering around the regression line.
(C) Correlation r measures the strength and direction only of linear association
(D) A correlation of 0.78 indicates a relationship that is 3 times as linear as one for which the correlation is 0.26.
(E) Outliers can greatly affect the value of r.
(D)
b = r(**sy/sx) where b is slope.
The standard deviations are always positive, so b and r have the same sign. Positive and negative correlations with the same absolute value indicate data having the same degree of clustering around their regression lines, on of which slopes up to the right and the other which slopes down to the right.
(D) is false because even though r=0.78 indicates a better fit with a linear model than r=0.26 we cannot say that the linearity is threefold.
(E) Correlation is sensitive to outliers.
Standard Deviation
If the standard deviation is 0:
(A) there is no relationship between the observations
(B) the average value is 0.
(C) all the observations are the same value.
(D) An error in calculation has been made
(E) None of the above
(C)
Mean
On a test, 25 students average 87 in one class; while 30 students in another class averaged 98. If the two classes are combined, what will be the average?
93
If every man married a woman exactly 3 years younger than he, what would be the correlation between the ages of married men and women?
(A) Somewhat negative
(B) 0
(C) Somewhat positive
(D) Nearly 1
(E) 1
(E)
r=1
Regression
Expenditure = 43 + 0.23(Age) with r=.27
What percentage of the variation in expenditures can be explained by looking at ages?
(A) 0.23%
(B) 23%
(C) 7.29%
(D) 27%
(E) 52.0%
(C)
The coefficient of determination r2 gives the proportion of the y-variance that is predictable from a knowledge of x.
r2 = square(0.27) = 7.29%
Median=270 and interquartile range=20
Which of the following is true?
(A) Fifty percent of the data are greater than or equal to 270
(B) Fifty percent of the data are between 260 and 280.
(C) 75% of the data are less than or equal to 280
(D) 250 ≤ mean ≤ 290
(E) The standard deviation is approximately 13.5
(A)
Combined standard deviation of two samples
Average American man has a mean height of 70 inches with a standard deviation of three inches and that the average American woman has a mean height of 65 inches with a standard deviation of two inches. Also assume that the number of men, N, is equal to the number of women. Then the mean and standard deviation of heights of American adults could be calculated as:
Mean = 67.5; standard deviation ≈ 3.57
Strategy: Nx = Ny in this case; the sample sizes cancel out when we write out the equation below, but this will not work if Nx≠Ny
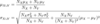
Data on age (in years) and prices(in $100) for ten cars of a specific model result in the regression line:
Price =250 - 30*Age
Given that 64% of the variation in price is explainable by variation in age, what is the value of the correlation coefficient r?
(A) -.64
(B) -.80
(C) .64
(D) .80
(E) There is insufficient information to answer the question
(B)
- r2 = 0.64* and we note that the slope of the regression line is negative. The correlation has the same sign as the slope; so:
- r=sqrt(.64)= -.8*
Which of the following is a true statement about the correlation coefficient r?
(A) A correlation of .3 means that 30 percent of the points are highly correlated
(B)


