Control Systems Ch. 2: Laplace Transform

Question 1

Major Types of Transforms

Answer 1

• Laplace Transform
• Inverse Laplace Transform
• z-Transform (discrete version of Laplace Transform)
• Fourier Transform (a subset of Laplace Transform, developed earlier)

Question 2

What is the Laplace Transform used for?

Answer 2

It is a well established technique for solving Differential Equations.

It transforms Differential Equations into Algebraic Equations which are easier to manipulate and solve.

Question 3

Basic Idea of using

Transforms

to solve Hard Problems

Answer 3

• Begin with the Hard Problem
• Apply a transform, obtaining an Easy Problem
  
  • Even if it isn’t exact, it is often still useful
• Solve the Easy Problem
• Perform an Inverse Transform on the solution to obtain a solution to the original Hard Problem

Question 4

Why are Laplace Transforms

applicable to physical systems?

Answer 4

A peculiarity of physical systems( LTI systems) is that they can be modeled by Differential Equations.

The Laplace Transform is able to transform the difficult differential equations into easier to solve algebraic equations.

Applying the Inverse Laplace Transform allows us to obtain a solution to the Differential Equations defining a system.

Question 5

Laplace Transform of a function:

Formal Definition

Answer 5

The Laplace transform of a function f(t), denoted as F(s), is defined as:

Question 6

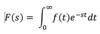
Relationship between

Laplace Transform

and

Fourier Transform

Answer 6

• Both equations are very similar
• The Laplace transform uses the term ‘s’, while the Fourier Transform uses the term “jω”
• The Laplace Transform was developed to overcome some limitations of the Fourier Transform
• It is basically the Fourier Transform with an additional term, e^-σt
• The expansion of “s” is actually some real number, σ, plus the “jω” term from the Fourier Transform:
  
  • s = σ + jω
• Mathematically, the Fourier Transform is a subset of the Laplace transform

Question 7

Why use Laplace Transform

instead of Fourier Transform?

Answer 7

• Fourier Transform is extremely useful for analyzing many kinds of systems
• But it has some shortcomings:
  
  • Not useful for studying stability of systems, which involves diverging signals
  • Fourier Integral does not converge for signals that diverge, because they are not absolutely integrable
• Laplace Transform overcomes this because of the exponential weighting, e^-σt
• It is able to converge on signals that the Fourier Transform does not converge on

Question 8

Laplace Transform:

Exponential Weighting

Answer 8

Laplace Transform uses Exponential Weighting, applying the term

e^-σt

• σ is some real number, the real part of s
• The value of σ determines if a signal is multiplied by a decaying or expanding exponential
• This allows us to choose σ such that the signal becomes convergent
• The region in the “s” plane where this infinite integral converges is called the Region of Convergence (ROC)

Question 9

Properties of the

Laplace Transform

(6)

(Name and Operation in Time and s domains)

Answer 9

Question 10

Laplace Transform Pairs:

f(t) = 1

Answer 10

Laplace Transform Pairs:

F(s) = 1/s

Question 11

Laplace Transform Pairs:

F(s) = 1/s

Answer 11

Laplace Transform Pairs:

f(t) = 1

Question 12

Laplace Transform Pairs:

f(t) = K

Answer 12

Laplace Transform Pairs:

F(s) = K/s

Question 13

Laplace Transform Pairs:

F(s) = K/s

Answer 13

Laplace Transform Pairs:

f(t) = K

Question 14

Laplace Transform Pairs:

f(t) = t

Answer 14

Laplace Transform Pairs:

F(s) = 1/s²

Question 15

Laplace Transform Pairs:

F(s) = 1/s²

Answer 15

Laplace Transform Pairs:

f(t) = t

Question 16

Laplace Transform Pairs:

f(t) = tⁿ

Answer 16

Laplace Transform Pairs:

F(s) = n! / sⁿ⁺¹

Question 17

Laplace Transform Pairs:

F(s) = n! / sⁿ⁺¹

Answer 17

Laplace Transform Pairs:

f(t) = tⁿ

Question 18

Laplace Transform Pairs:

f(t) = e^-at

Answer 18

Laplace Transform Pairs:

F(s) = 1 /( s+a )

Question 19

Laplace Transform Pairs:

F(s) = 1 /( s+a )

Answer 19

Laplace Transform Pairs:

f(t) = e^-at

Question 20

Laplace Transform Pairs:

f(t) = e^at

Answer 20

Laplace Transform Pairs:

F(s) = 1 /( s - a )

Question 21

Laplace Transform Pairs:

F(s) = 1 /( s - a )

Answer 21

Laplace Transform Pairs:

f(t) = e^at