Control - Exam Deck

Question 1

FT of Cosine

Answer 1

Question 2

FT of Sine

Answer 2

Question 3

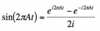
Laplace transform of this combination

Remember this!!

Answer 3

Question 4

State Space - Volumetric balance Equation

Answer 4

Question 5

Transfer functions and harmonic inputs

Do c)

Answer 5

Question 6

Do b)

Answer 6

Question 7

Why do we use State Space?

Answer 7

• Easier to manage computationally
  
  • more efficient than inputting higher order derivatives
• matrix describes behaviour of the system and the properties of th matrix allows for convenient analysis of the behaviour e.g. with the determinant we gain info on stability, eigen values tell us abut stability and the behaviour the system will follow.

Question 8

Do a)

Answer 8

• Key things to remember here:
  
  • Laminar flow → proportional to the pressure difference between the ends
  • flow in to tank 1 through the connecting pipe is proportional to the difference in level, h₂ - h₁
    
    • _​this shows why h₁ is negative in the eq for dh₁/dt
    • remember we’re dealing with flow and the tanks will aim to reach an equillibrium between it eachother.
  • the value of 3 is just a constant, refer to slide 10 of chapter 2 part 1

Question 9

What is the inverse of a 2x2 matrix?

Answer 9

• note the how a and d are flipped and c b values are just negated
• and the determinant is based on old matrix (negative values of c and b are not included)

Question 10

Decomposing a s-domain function into a partial fraction: Finding the unkown coefficients

Answer 10

1. Full method is as follows:
2. Find the partial fraction of the s-domain function in question
3. Equate the partial fraction to the original function
4. For an unkown coefficient,multiply by the dividing factor
   
   1. On the PF side this moves the factor to the other terms while on the original side this just cancels the factor out.
5. By plugging in the vaue for s that makes the factor 0, you cancel out the other terms and are left with a constant value on the LHS equal to the constant coefficient in question
6. Repeat this process for the remaining unkown constants.

Question 11

Final value from the s-domain: If all that is required is the final or steady state value of the signal f(t), what is the equation?

Answer 11

Question 12

Final value in the time domain:

Answer 12

Set derivatives to zero for the steady state solution

Question 13

Do the first part: deriving the matrix equation shown.

Answer 13

Question 14

Do the second part: final value theorem

Answer 14

Question 15

Draw the block diagram

Answer 15

Question 16

What equation should you use to calculate values in a routh array?

Answer 16

-(1/corner_value) times determinant of 2x2 matrix in question

make sure to multiply a to d and b to c, traditional determinant calculation.

Forget about the other method…

Also key thing to remember is the negative.

Question 17

If you get a 0 for a place in the first column of a routh array calculation what do you need to do?

Answer 17

place a variable that represents a very small positive value, like ε.

Question 18

Use the Routh Hurwitz stability method to investigate the stability of the closed loop system

Answer 18

Question 19

Use the Routh Hurwitz stability method to investigate the stability of the closed loop system

Answer 19

Question 20

When looking at stability conditions of a closed loop system with a undefined K, what is the stability of the system if K is only found for the s⁰ value in the first column?

Answer 20

Stable for all K values.

s⁰ does not affect the stability condition.

Question 21

3. A control engineer should have intuition about what types of systems are potentially unstable and those which will never go unstable. Use the results of Q2 to decide if (a) second order systems can ever become unstable when feedback is applied (b) the likely effect of including an extra integrator (a 1/s factor) in the forward path.

Answer 21

Question 22

Do d)

Answer 22

• Feedforward requires the disturbances to be anticipated or measured before they have an impact on the controlled variable which is temperature in this case.
• Feedforward is not feasible in a basic control system because (for instance) on a cloudy day one does not know when the sun may come out and start to heat the house.
• An advanced environmental system might make it possible, however.
  
  • For instance, if the house had solar panels changes in the rate of electricity generation would give a few minutes warning of changes in temperature due to the level of sun hitting the house.
  • Another example would be if a window were opened. A sensor on the window could cause the controller to increase the heat input from the furnace in anticipation of cool air coming into the house through the window.
• Disturbances such as the daily variations in temperature are slow compared to the response time of the control system and can be adequately dealt with by feedback even though they could be anticipated in advance.

Question 23

State the final value theorem and explain its derivation. [6 marks]

Answer 23

Question 24

What is the (1+ s 𝜏) format?

Answer 24

when s is divided by a value

not multiplied.

Question 25

For a class zero system with a E(s) function that is in the (1+ s 𝜏) format, what is the output of the final value theorem going to be?

Answer 25

1/ (1 + Ka)

Question 26

Steady state errors

Answer 26

Question 27

If the input is a unit step, show that the use of the phase lag compensator gives the benefit of reducing the steady state error by a factor of 4.7 compared to the case when there is no phase lag compensation.

Answer 27

Question 28

Calculate transfer function

Answer 28

Question 29

Time delay

Answer 29

Question 30

Use a partial fraction expansion to determine the time domain signal

Answer 30

Question 31

Steady state analysis

Answer 31

Question 32

State how the class of a control system may be determined from an inspection of the system block diagram, if the transfer functions of its components are known. In what way is a class 1 system better than a class 0 system?

Answer 32

The number of integrators determines the class of the system. A class-N system has N integrator components (i.e., N poles at zero, or 𝑠 ⁻¹ terms). If feedback is employed in a class-1 system, the system, having one integrator in the forward path, can respond accurately to a step input with no steady-state error. Further, there is an error of 1 / K (with K the gain in the forward path) in the response to a ramp input if feedback is employed. That is, a class-1 system can track ramp inputs as well, but with non-zero error.

On the other hand, a class-0 system → non-zero error for step inputs but it cannot track ramp inputs.

Question 33

Explain what is meant by a pole in a transfer function. Describe what features of the output of a system are determined by the poles when the input to the system is a unit step.

Answer 33

The poles are the values of s where G(s) becomes infinite.

Question 34

What is the function of a ramp input?

Answer 34

Look it up.

Question 35

Steady state error to a unit step for a type-1 system?

Answer 35

steady state error to a unit step is zero (regardless of the value of 𝐾)

Question 36

Class zero and step input

Answer 36

Class zero system has a steady state error in response to a step input. To reduce the error the gain K should be large.

Question 37

Steady state error: Class One and ramp input

Answer 37

There is an error of 1 K in the response to a ramp input

Question 38

What is the equation for a unit ramp

Answer 38

1/s²

Question 39

Find the final value for the closed loop response (with negative unity feedback) to a unit step input for:

Answer 39

class 1 output is unit for step input

class 0 is K/(1+K)