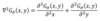Computer Vision Flashcards
Perspective projection
- y / Y = f / Z -> y = fY/Z
- Similarly, x = fX/Z
- (X,Y,Z) -> (x,y): R³ -> R²
Coordinate conversion
- Cartesian to homogenous
1) P = (x,y) -> (x,y,1)
2) P ∈ R² -> P̃ ∈ P² - Homogenous to cartesian
1) P̃ = (x̃, ỹ, z̃) -> P = (x,y)
Sidenote: x = x̃/z, y = ỹ/z
Perspective projection equation
2D point = [x̃;ỹ;z̃]
Projection matrix = [f 0 0 0; 0 f 0 0; 0 0 1 0]
3D point: [X; Y; Z; 1]
- 2D point = projection matrix * 3D point
- x̃ = fX, ỹ = fY, z̃ = Z
- To convert back to cartesian, divide by third coordinate (i.e., x = fX/Z, y = fY/Z)
Intrisic model
- An upgrade from the simple projection model
- Includes the following properties:
1) Change of coordinate meters to pixels
2) Focal lengths are independent for x and y (defined as fₓ and fᵧ)
3) A skew , s , is included
4) Optical centre (cₓ, cᵧ) is included
Equation for intrisic model
[fₓ s cₓ 0; 0 fᵧ cᵧ 0; 0 0 1 0] = [1/pₓ 1/pₛ cₓ; 0 1/pᵧ cᵧ; 0 0 1] * [f 0 0 0; 0 f 0 0; 0 0 1 0]
Extrinsic model
- Also known as the pose
- Consists of a 3x1 3D-Translation vector t
- Consists of a 3x3 3D-Rotation matrix R
Overall camera matrix
- Considers both intrinsic and extrinsic calibration parameters together
- [x̃;ỹ;z̃] = [fₓ s cₓ; 0 fᵧ cᵧ; 0 0 1]*[R3D t]*[X;Y;Z;1]
Lens cameras
- Larger aperture = more light = less fous
- Less shutter speed = less exposure time = less amount of light reaching the sensor
Focal length
- Equation: 1/f = 1/zᵢ + 1/z₀
- f = focal length
- z₀ = where object is
- zᵢ = where image is formed
A/D
- Analogue to Digital conversion
- Spatially-continuous image is sampled (CCD or CMOS) by a few pixels
- Pixel values are then quantized e.g. 0 (black) to 255 (white)
Shannon Sampling Theorem
- Used to choose sampling resolution
- If signal is bandlimited, then fₛ ≥ 2 * fₘₐₓ, where:
1) fₛ = sampling (aka Nyquist) rate
2) fₘₐₓ = maximum signal frequency - This equation is enough to guarantee that the signal can be perfectly linearly reconstructed from its samples
- If signal is not bandlimited, then use analogue low-pass filter to clip frequency contents fᵤₜ ≤ fₛ/2
Quantization
- Used to determine bit rate
- In audio, this would be the number of bits sent per second (CD’s are usually 16-bit)
- In imaging, this would be in terms of coding the value of pixels (Images are usually 24-bit)
Compressed sensing
Steps
1) Regular sampling (namely Shannon)
2) Random sampling
- Used to collect a subset
- Complexity: M = O (K log (N/K))
3) Reconstruction
- Obtain x from y
4) Sparse approximation
- Is typically a non-linear reconstruction
- Should have a prior awareness
- Equation for prior awareness:
Compressed sensing hallmarks
- Stable
1) Acquisition and recovery is numerically stable - Assymetrical
- Democratic
1) Each measurement carries the same amount of information - Encrypted
1) Random measurements are encrypted - Universal
1) Same random patterns can be used to sense any sparse digital class
Convolution steps
1) Flip filter vertically and horizontally
2) Pad image with zeros
3) Slide flipped filter over the image and compute weighted sum
Convolution distributive property
- Consider an image I
- Consider two filters g and h
- Image I is convolved by filters g and h and the results are added together (i.e. Î = (I * g) + (I * h))
- Distributive property states that ((I * g) + (I * h)) ≡ (I * (g + h))
Correlation
- No flipping of kernel
- No padding image
- Just slide filter over the image and compute weighted sum
Normalized correlation
-Used to measure similarity between a patch and image at location (x,y)
SSD
- Stands for Sum of Squared Differences
- Calculates the moving difference between the intensities of a patch and an image
- Given a template image/patch, fins where it is located in another image by finding displacement (x*,y*) which minimises SSD cost
Low-pass filter
- Smooths (blurs) an image by (weighted/ unweighted) averaging pixels in its neighborhood
- Also known as a Gaussian filter
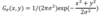
High-pass filter
- Computes finite (weighted/unweighted) differences between pixels and their neighbors
- Extracts important low-level information: intensity variations
- HP filters have zero mean and remove DC component from images
- Example of HP filter is edge detection
- Horizontal edge: [-1 -1; 1 1]
- Vertical edge: [-1 1; -1 1]
Derivative of Gaussian
- A high-pass filter
- Used to implement nth order image differences
- For example, with a second order derivative
- (∂2I)/(∂2x) ≈ f1∗f1∗I
- (∂2I)/(∂2y) ≈ f2∗f2∗I
- For example, with a second order derivative
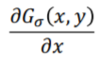
Laplacian of Gaussian filter
- A high-pass filter
- Used to implement 2nd order image differences
- In the equation, ∇² represents the Laplacian operator
- ∇²f = (∂²f / ∂x²) + (∂²f / ∂y²)
Subtraction of filters
- Typically used for sharpening
- ISharp(x,y) = I(x,y) - α(I ∗ ∇²Gσ(x,y))
Gaussian vs mean filtering
- Gaussian blur results in less artifacts
-
Anti-aliasing
- Aliasing = appearance of artefacts due to loss of image data
- To solve, apply a low-pass filter to an image before downsizing an image
Difference of Gaussians (DoG)
- DoG{I,σ₁,σ₂} = gσ₁ ∗ I - gσ₂ ∗ I = (gσ₁ - gσ₂) ∗ I
- Extracts “edges” at multiple scales i.e. the information difference between two scales
Image resampling (stretching)
- Increase image size
- Interleave the small image with zeros
- Apply a low-pass filter
- This linearly interpolates between the pixels
Canny edge detection
- The most wildely used edge detector
Steps
1) Compute a robust gradient of the image (i.e. using Gaussian differentiation)
- Compute gradient’s magnitude and direction
2) Apply non-maxima suppression for edge-thinning - Keep largest edge (i.e. local maxima in a neighborhood) across gradient direction, suppress the rest
3) “Hysteresis thresholding” to discard non-connected components - Define two thresholds: T-high and T-low
- ‘Track’ a strong edge from T-high, keep connected edges above T-low, discard the rest
- Note: Step 2&3 discard many False Positives to get clean edges*
Non-maxima suppression
Check if pixel is local maximum along gradient direction (in a window); if yes then keep it & discard other candidates
Hysteresis thresholding
- Threshold the gradient magnitude with two thresholds: T-high and T-low
- Strong Edges start at edge locations with gradient magnitude > T-high
- The values in between may be an edge (blow T-low not)
- Continue tracing that edge until gradient magnitude falls below T-low, keeping only connected components in this range
Effect of σ
- σ = Gaussian kernel spread/size
- The choice of depends on desired behavior
1) Large σ detects large scale edges
2) Small σ detects fine features
Intensity-based matching process
- Select patches
- Slide them across the image
- Score the SSD & report minimizer
Good features of intensity-based matching
Locality
- In a “neighbourhood” pixels reveal important structures
- Shift-invariance (e.g. patch space vs. original image)
Efficiency
- Features extraction in real-time is possible Quantity • Instead of O(106) pixels, e.g. O(103) features to match. • Search in real-time is possible Distinctiveness • Can differentiate a large database of objects Building invariances • Invariant to image transformations e.g. shift, rotation, scale, deformations,… • robust to clutter, noise and occlusion
Gradients behavior in a patch equations
Gradients behavior in a patch analysis
PCA
- Stands for Principal Component Analysis
-
Harris corners
- In practice computing eigen values is not very fast
- Harris instead proposed to approximate the process by the following functions:
If R scores higher than a threshold is a corner candidate
Harris detector process
- Compute directional derivatives Ix, Iy and IxIy at each pixel (and smooth them with Gaussian filters).
- Compute the Structure Matrix in a window/patch around each pixel
- Compute corner response function R
- Threshold R
- Find local maxima of response function (non-maximum suppression)
SIFT
- Stands for Scale Invariant Feature Transform
- Used in object recognition as it’s powerful, especially for well-textured objects
SIFT matching process
- Each image has 100 to 1000 SIFT descriptors (instead of 1M pixels)
- Each is represented by 128 numbers vector φ
- SSD can be used for measure: ∑_(i=1)^128 (φi(1) – φi(2))
- Feature matching = minimizing SSD (search)
- fast KD-tree type search can be adopted
- SIFT feature matching can run in real-time!
SIFT fine-tuning
Feature matching still returns a set of noisy correspondences
Refinements:
- Discard weak matches with SSD(φ(1),φ(2)) > threshold
- Keep only clear matches i.e. R << 1
- R = SSD(φ(1),φ(2))/SSD(φ(1),φ′(2))
- φ(2) = best SSD match to φ(1) in second image
- φ′(2) = 2nd best SSD match to φ(1) in second image
- R gives large values ~ 1 for ambiguous matches
- R = SSD(φ(1),φ(2))/SSD(φ(1),φ′(2))
- Discard inconsistent matches; for which we need to know something about the geometry of the scene
Applications of SIFT
Without geometry
Object recognition
With geometry
- Building panoramas
- Extract & match SIFT features
- Use matched pairs to learn a (homography) mapping which holds for all points in two images
- Apply the mapping to stitch two images
- 3D reconstruction
- Use SIFT to find dense correspondences between multiple images of a scene
- Use matched tuples (+ non-planar geometry) to estimate 3D shape
SIFT vs Harris
- SIFT has scale invariance, Harris doesn’t
- Both have shift, rotation and illumination variance
- SIFT provides descriptors, Harris doesn’t
Measuring performance of a feature matcher
- TP (true positive): number of correct matches
- FN (false negative): number of matches that were not correctly detected
- FP (false positive): number of proposed matches that are incorrect
- TN (true negative): number of non-matches that were correctly rejected
- TP rate = TP/(TP+FN) = TP/P
- FP rate = FP/(FP+TN) = FP/N
- Accuracy = (TP+TN)/(N+P)
Taylor Expansion of DoG
Has three purposes:
1) Achieves sub-pixel accuracy for keypoint localiazion
2) Reject edges
3) Reject low-contrast keypoints
Key point localisation
Detect maxima and minima of DoG in scale & space
- Each point is compared compared with to the 26 pixels in the current and its adjacent scales
- Detected if larger/smaller than all of the 26 pixels
- Extrema must be stronger than a threshold to reject candidates with low contrast
Discarding of low-contact points
Elimination of edge responses
- For candidates, construct a 2x2 (Hessian) matrix:
- [Dxx Dxy; Dxy Dyy]
Orientation Assignment
Calculating iterations from RANSAC
S = iterations to be calculated
K = points in model
q = 1 - probability of choosing outlier
Solving a camera matrix with a linear system
- This involves the factoring of knowns and unknowns and writing it as a linear system
- System: A*[C11; C12; C13; C14; … C33] = b
- Each correspondence adds two rows to A: one for the x-coordinate and one for the y-coordinate of the point
- At least 6 correspondences are needed to compute all 1 1 unknowns in the camera matrix
- Number of rows in A = 2n
- Number of columns in A= 11
- Number of rows in B = 2n
- Number of columns in B = 1
Solving triangulation using linear systems
Given Multiview correspondences {p1,p2,…} in calibrated cameras {C1,C2,…}, reconstruct the corresponding 3D point P = [X, Y, Z, 1] compliant with the projection model in every views
Example of epipolar lines
- Converging views
- Span the whole 3D space by all epipolar planes:
- This gives all epipolar lines pairs
- All epipolar planes intersect at the baseline
- All epipolar lines converge to epipoles because tje baseline planes intersect at the baseline, and the baseline’s projection in each view is the epilole
- To span the whole 3D space, infinitely epipolar planes need to be considerd
- Since all of these planes share the same baseline, they can be viewed as they rotate along the Baseline axis to span the 3D space
- If the 3D space is spanned in this way, and each epipolar plane is projected to the two image views, we will get a set of dual epipolar lines that span the images of each camera
- They are dual because a point in red line in one camera corresponds to a red line in other camera i.e. it finds it’s correspondences there.
Examples of epipolar lines #2
- Motion parallel to image plane
- This is a typical scenario in stereo vision, parallel views with motion
- However, there is no convergence due to the views being parallel with motion
- Each view contains parallel epipolar lines
- Epipoles are at infinity
Examples of epipolar lines #3
- Motion perpendicular to image plane
- Epipoles have same coordinates in both images
- Epipolar lines radiate from the epipoles
Useful non-local prior: Uniqueness
For any point in one image, there should be at most one matching point in the other image
Useful non-local prior: Ordering
Corresponding points are in the same order in both views
Useful non-local prior: Piecewise smoothness
Disparity values are expected to change slowly for the most parts (except for the edges)
Energy minimisation framework
Used to enforce piecewise smoothness
Pros
- Generality
- Does not need training data
- Rather uses geometry knowledge (physics)
Cons
- Solving optimisation is time-consuming
Process
Edata = data fidelity
Esmooth = data smoothness
D = disparity
Weak classifier
- Weak classifiers can be defined for each boxlet feature
- Weak classifiers individually have high detection errors
- They are parameterised by some threshold value and some polarity value, which has a difference of 1 in comparison to the threshold
- A problem with such a classifier is that due to individual processing of features, it is not enough to correctly detect a “face” or “not face”
Fisher’s Separability
- µ = mean
- σ = standard deviation (i.e., σ2 = variance)
Graph-partitioning
- Idea: graph-partitioning
- Similar pixels have similar values (e.g. RGB) and are spatially close to each other i.e. neighbors
- A graph represents an image where the nodes represent the pixels & edges measure affinity (similarity) between pixels
2D to 2D transformations
3D to 3D transformations
