Computer Science Flashcards
(24 cards)
What is Big O?
It’s the upper bound on the time an algorithm takes to operate.
What is bi Ω?
It is the lower bound on the tome a algorithm takes to operate.
What is big Θ?
An algorithm is Θ(Ν) if it’s both O(N) and Θ(N).
Θ(N) gives a tight bound on runtime. In industry, we use this as O instead.
What is an ArrayList and what is it’s amortized time for adding an element?
It is a dynamically resizing array.
The array copies all it’s elements into a new array when it runs out of space.
The amortized time of adding an item is O(1).
Because amortised it’s O(x+x/2+x/4+x/8+...+1) which is roughly O(2X).
Therefore the amortized time is O(1). ????
What is a Log N runtime?
It is a runtime that takes as many steps as the logarithm of the length of the dataset.
A good example is a binary search. On a data set of 16 elements, it would take up to 4 steps to find an item.
N = 16
N = 8
N = 4
N = 2
N = 1
log 2 16 = 4
Can you describe an O(2^N) runtime?
It can be a recursive runtime that each recursion makes 2 recursive calls.
If such an operation would create nodes in a tree it would make a balanced binary tree so we can actually express this as:
F(1)
F(2) <
F(1)
F(3) <
F(1)
F(2) <
F(1)
F(4) <
F(1)
F(2) <
F(1)
F(3) <
F(1)
F(2) <
F(1)
What is the runtime of
for i in array
for j in array
print(i + j)
O(N^2) Because it prints all possible combinations.
What is the big O of…
void printUnorderedPairs(int[] arrayA, int[] arrayB) {
for (int i = 0; i < arrayA.length; i++) {
for (int j = 0; j < arrayB.length; j++) {
if (arrayA[i] < arrayB[j] ) {
System.out.println(arrayA[i] + "," + arrayB[j]);
}
}
}
}
0(ab) because the iteration is between two different datasets.
What is the big O of…
void printUnorderedPairs(int[] arrayA, int[] arrayB) {
for (int i = 0; i < arrayA.length; i++) {
for (int j = 0; j < arrayB.length; j++) {
for (int k = 0; k < 100000; k++) {
System.out.println(arrayA[i] + "," + arrayB[j]);
}
}
}
}
O(ab) because the third loop is constant time.
What is the big O of…
void reverse(int [] array) {
for (int i = 0; i < array.length / 2; i++) {
int other = array.length - i -1;
int temp = array[i];
array[i] = array[other];
array[other] = temp;
}
}
0(N)!
The fact that it only goes through the array(in terms of iterations) does not impact the big O time.
Is O(N + P) where P < N/2 equivalent to O(N)?
Yes,
if P < n/2, then we know that N is the dominant term, so we can drop the O(P).
Is O(2N) equivalent to O(N)?
Yes,
since we drop constants.
Is O(N + log N) equivalent to O(N)?
Yes,
O(N) dominates O(log N), so we can drop the O(log N).
Is O(N + M) equivalent to O(N)?
No,
because there is no established relationship between N and M, so, we have to keep both values.
Suppose we had an algorithm that:
- took an array of strings
- sorted each string
- then sorted the full array
What would the runtime be?
It is O(a*s(log a + log s)).
- let s be the length of the longest string.
- let a be the length of the array.
- Sorting each string is O(s log s). We have to do this for every string(and there are a number of strings), so that’s O(a * s log s),
- We have to sort all the strings because we have to compare the pairs that operation is O(a*s log a)
- If you add up this two parts, you get
O(a*s(log a + log s))
This is it, There is no way to reduce it further.
What is the runtime of
int sum(Node node) {
if (node == null) {
return 0;
}
return sum(node.left) + node.value + sum(node.right);
}
It is O(N) because we iterate all the nodes of the tree. The tree is a balanced tree therefore if there are N nodes the depth is roughly log N. By the equation above we get O(2^log N) so, let P = 2^log N -> log 2 P = log 2 N -> P = N -> 2^log N = N therefore, the runtime of this code is O(N), where N is te number of nodes.
What is the runtime of:
boolean isPrime(int n) {
for (int x =2; x * x <= n; x++) {
if (n % x == 0) {
return false;
}
}
return true;
}
It’s O(√n).
The for loop will start when x = 2 and end when x*x = n
Or in other words, it stops when
x = √n
The following computes n! (n factorial).
What is it’s time complexity?
int factorial(int n) {
if (n < 0) {
return -1;
}
else if (n == 0) {
return 1;
}
else {
return n * factorial(n - 1);
}
};
O(n). This is a streight recursion from n down to 1.
This code prints the permutations of a string.
void permutation(String str) {
permutation(str, "");
}
void permutation(String str, String prefix) {
if(str.length == 0) {
System.out.println(prefix);
} else {
for (int i=0; i < str.length(); i++) {
String rem = str.subsstring(0, i) + str.substring(i + 1);
permutation(rem, prefix + str.charAt(i));
}
}
}
it is O(n!)
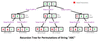
What is Union By Rank?
It when merging two trees into one and the shorter one is merged under the root of the taller one.
This technique keeps the tree shallow.
What are disjoint sets?
Two sets are said to be disjoint sets if they have no element in common.
What O(log * n) an efficient algorithm?
log star theoretically speaking is not bound, however, it is at most five for all practical values of n.
That makes for a very efficient operation in practice.
How many bits is an IP v4 address?
An IP v4 address can be stored as a 32 bits binary integer.
Each segment is an integer from 0 to 255. This is a range of values 28
For example the IP
172.16.254.1 === 10101100.00010000.11111110.00000001
How do you calculate the decimal value of an IPv4 address?
IP[1]*224 + IP[1]*216 + IP[3]*28 + IP[4]


