Complex Numbers Flashcards
(20 cards)
What is Euler’s equation for complex numbers?

What is a complex (aka Argand) plane?
It’s just like the normal Cartesian plane, but Re(z) is the horizontal axis and Im(z) is the vertical axis.

Complete the following rule for complex conjugates.


Complete the following rule for complex conjugates.


What is the modulus of a complex number?

It’s the magnitude of the vector from the origin to point z on a complex plane.

Complete the following property of a modulus:


Complete the following property of a modulus:


Complete the following property of a modulus:


Complete the following property of a modulus:


What is the argument, arg z, of a complex number?
The argument of a complex number is the angle between its vector and the positive real axis.
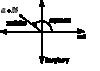
How do you represent a complex number in polar form?

How do you write the complex conjugate of z in polar form?

According to De Moivre’s Theorem,


How many solutions are there for the following equation?

The n nth roots of c are the solutions.
What is the modulus for all roots of the following equation?

All of the roots will have modulus,

If you are asked to simplify something with a z in the denominator, what is 1 good stragety?

- Multiply the denominator to the other side of the equation and solve for z.
- In the last moment change z to the form required.

If you are asked to isolate the real (or imaginary) part of an expression of complex numbers, what is a good strategy?

- Simplify the denominator.
- Multiply by the complex conjugate of the denominator to get rid of the fraction.
- Group the real parts together and the imaginary parts together.

How many complex solutions must an odd polynomial have? (How many complex solutions are there to x^n=1 if n is odd)?
Odd polynomials may not have any complex roots. However, if there exists any complex root, then they must always come in pairs.
If you know that w is a non-real solution to z^3=1, how can you best use this to simplify expressions of w?

- Recall that both w^3=1 and w*^3=1.
- Replace any 1s in the expression with w^3.
- Factor and rearrange, somehow taking advantage of the fact that w^3-1=0.

If you’re given distinct roots of a complex equation/function, how do you know the other roots?

For an even function, the roots always come in conjugate pairs.



