Circular Motion and SHM Flashcards
What kind of motion will a pendulum perform?
Simple harmonic motion
If the graph of displacement is cos(x), what will the respective graphs of velocity and acceleration look like SHM?
Velocity as -sin(x)
Acceleration as -cos(x)
Same as SVA in maths for differentiating / integrating
Describe a freely oscillating object
It oscillates with a constant amplitude because there is no external force acting on it
(Its energy is constant)
What is natural frequency?
The frequency of free oscillations of an oscillating system.
What are forced vibrations?
Making an object oscillate at a frequency that is not it’s natural frequency
When does resonance occur?
When the frequency of driving force or oscillation matches the natural frequency of the system.
What is the outcome of resonance?
An increase in amplitude of the system’s oscillation.
What is damping?
The term used to describe the removal of energy from an oscillating system.
What are the three levels of damping?
Light
Heavy
Critical
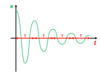
Describe the motion of a lightly damped system
The system oscillates over a long time frame before coming to rest.
The amplitude of the oscillations exponentially decay. But the time period of oscillations remains constant
Describe heavy damping (over damping)
System not allowed to oscillate.
Slowly returns to equilibrium.
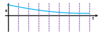
Describe critical damping
The oscillating system returns to the zero position of the oscillation after one quarter of a time period.
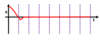
What are the two conditions for SHM?
- Acceleration must be proportional to displacement
- Acceleration must be opposite to displacement
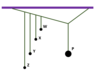
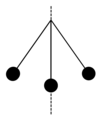
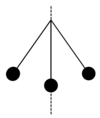
Label up the maximum and minimum velocities and accelerations on the simple pendulum…
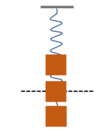
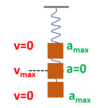
Label up the maximum and minimum velocities and accelerations on the mass spring system…
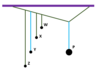
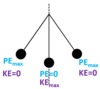
Label up the maximum and minimum potential and kinetic energies on the simple pendulum…
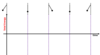
What are the kinetic energy, potential energy and total energy lines for one cycle of SHM?
When do you use?
x=Acos(wt)
When do you use?
x=Asin(wt)
x=Acos(wt) -> displacement in SHM when x=A when t=0
x=Asin(wt) -> displacement in SHM when x=0 when t=0
MUST BE IN RADIANS
How do you calculate KEmax or PEmax or ET in SHM?
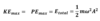
What two factors affect the time period of a mass spring system in SHM?
- Mass on the end of the spring
- Spring constant (stiffness) of spring
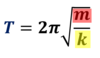
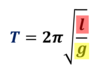
What two factors affect the time period of a simple pendulum in SHM?
- Length between top of string and centre of bob
- Gravitational field strength
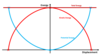
What could the graph of energy against displacement look like in SHM?
Does circular motion count as SHM?
When projected onto a flat surface, yes it does
When a SHM system is lightly damped what happens to its amplitude and time period?
Amplitude decreases (as it loses energy)
But time period remains constant
How is natural frequency determined for a mass spring system?
How is natural frequency determined for a simple pendulum?
What happens if the frequency of driving force is less than the natural frequency of a system?
f>f0
Low amplitude oscillations
Force and system oscillate with a constant phase difference of 0
What happens if the frequency of driving force matches the natural frequency of a system?
f=f0
Resonance occurs
Large amplitude oscillations
Force and system oscillate with π/2 constant phase difference
What happens if the frequency of driving force is more than the natural frequency of a system?
f>f0
Low amplitude oscillations
Force and the system oscillate with a constant phase difference of π
The graph below shows driven oscillations with varying frequencies.
Add two lines if the system is:
- Undamped (free oscillations)
- Over damped
For Barton’s pendulum which two balls oscillate?
P and Y because they have the same length
So natural frequency of y matches frequency of driving force from P
Y resonates and its amplitude is the largest with a phase difference of π/2 compared to P
How does the time period differ for two pendulums of different amplitudes?
Time period is the same for both pendulums.
Time period is independent of amplitude
What are some examples of simple harmonic motion?
- A pendulum
- A mass bouncing on a spring
- Modelling atomic bonds
What does KEmax equal?
KEmax = PEmax = Total energy = ½mω2A2
How do you calculate total energy at any point in SHM?
KE + PE at that point
When do pendulums undergo SHM?
When θ is small (less than 10 degrees / 1/18π radians)
Describe damping forces and their relation to velocity
Damping forces always oppose motion
Damping forces ∝ v2
Therefore, damping forces are max at x=0 and min at x=A
What are forced oscillations?
Oscillations produced by an external periodic force that has its own associated frequency
What will happen if pendulum y on Barton’s pendulum is released, in reference to the shorter pendulum x?
X has a shorter length than y
Therefore, x has a larger natural frequency
X will oscillate with a smaller amplitude and phase difference of 0 radians
What will happen if pendulum y on Barton’s pendulum is released, in reference to the longer pendulum z?
Z has a greater length than y
z has a smaller natural frequency than y
Z oscillates at a lower amplitude with phase difference π radians
If the graph of displacement is sin(x), what will the respective graphs of velocity and acceleration look like for SHM?
Velocity is cos(x)
Acceleration is -sin(x)
Same as SVA in maths for differentiating / integrating
What angle unit must you use for SHM?
Radians
