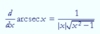Chapter Three: Derivatives

Question 1

limit definition of a derivative

Answer 1

Question 2

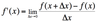
conditions of differentiability

Answer 2

1. the function must be continuous on the interval over which you are differentiating (no removable discontinuities)
2. the left and right-hand derivatives must be equal (no cusps, corners, or jump discontinuities)
3. the limit as x approaches c, where c is the point which is being differentiated, cannot be positive or negative infinity (no vertical tangent lines)

Question 3

power rule

Answer 3

f’(x) = ax^a-1

Question 4

product rule

Answer 4

p’(x) = f(x)g’(x) + g(x)f’(x)

the first times the derivative of the second, plus the second times the derivative of the first

Question 5

quotient rule

Answer 5

q’(x) = (g(x)f’(x) - f(x)g’(x)) / (g(x))²

the bottom times the derivative of the top, minus the top times the derivative of the bottom, all over the bottom squared

Question 6

chain rule

Answer 6

f’(x) = (derivative of outside function)(derivative of inside function)

Question 7

f’(x) of cscx

Answer 7

-cscxcotx

Question 8

f’(x) of secx

Answer 8

secxtanx

Question 9

f’(x) of cotx

Answer 9

-csc²x

Question 10

f’(x) of sinx

Answer 10

cosx

Question 11

f’(x) of cosx

Answer 11

-sinx

Question 12

f’(x) of tanx

Answer 12

sec²x

Question 13

f’(x) of a^x

Answer 13

a^xln(a)

note: if the power is a function, and not just x, it must also be differentiated, and multiplied by this because of the chain rule

Question 14

f’(x) of e^x

Answer 14

e^x

Question 15

f’(x) of ln(x)

Answer 15

1/x

note: if the argument of the natural log function is more complicated than just x, it must be differentiated as well by the chain rule

Question 16

f’(x) of y = log_bx

Answer 16

1 / (lnb)x

Question 17

formula for the derivative of an inverse function

Answer 17

in english: the derivative of g(x), where g(x) is the inverse of the function f(x), is equal to the reciprocal of the derivative of f(x), evaluated at g(x)

or

the value of the derivative of the inverse function evaluated at b equals the reciprocal of the derivative of the original function evaluated at a

Question 18

(f^-1)’(b) =

Answer 18

1 / f’(a)

Question 19

f’(x) of arcsinu

Answer 19

in english: the derivative of arcsin(u) is equal to 1 over the square root of 1 minus u squared

derivation: this formula is an extension of the Pythagorean Theorem. To derive:

1. multiply y = arcsinu by sin to get siny = u
2. take the derivative of both sides to get cosy times dy/dx = du/dx
3. isolate dy/dx
4. rewrite as y’ = u’/cosy
5. use a reference triangle to determine that cosy = √(1-u²)
6. write the final formula: y’ = 1/√(1-u²)

Question 20

f’(x) of arccosu

Answer 20

in english: the derivative of arccosx is equal to negative 1 over the square root of 1 - u squared

To derive:

1. multiply y = arccosu by cos to get cosy = u
2. take the derivative of both sides to get -siny times y’ = u’
3. isolate y’
4. rewrite as y’ = -u’/siny
5. use a reference triangle to determine that siny = √(1-u²)
6. write the final formula: y’ = -1/√(1-u²)

Question 21

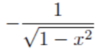
f’(x) of arctanu

Answer 21

in english: the derivative of arctanu is equal to 1 over 1 plus u squared

To derive:

1. multiply y = arctanu by tan to get tany = u
2. take the derivative of both sides to get sec²y times y’ = u’
3. isolate y’
4. rewrite as y’ = u’/sec²y
5. use a reference triangle to determine that sec²y = (√(1+u²))²
6. write the final formula: y’ = 1/(1+u²)

Question 22

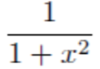
f’(x) of arccotu

Answer 22

in english: the derivative of arccotu is equal to negative 1 over 1 plus u squared

Question 23

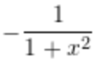
f’(x) of arccscu

Answer 23

in english: the derivative of arccscu is equal to negative 1 over the absolute value of u times the square root of u squared minus one

Question 24

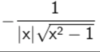
f’(x) of arcsecu

Answer 24

in english: the derivative of arcsecu is equal to 1 over the absolute value of u times the square root of u squared minus 1

Question 25

what is the derivative of any linear function?

Answer 25

a constant

Question 26

log_ab =

Answer 26

(lnb) / (lna)

Question 27

tip for logarithmic differentiation

Answer 27

when simplifying the derivative, be sure to eliminate all fractions in the expression. This will also likely affect the leading exponent on the term as well.

Question 28

y = log_ab

Answer 28

a^y = b

Question 29

f'(x) of |x|

Answer 29

|x| / x where x ≠ 0

Question 30

steps for implicit differentiation (differentiating relations)

Answer 30

1. differentiate both sides of the equation with respect to x 2. collect all terms that contain dy/dx on one side of the equation, leaving the remaining terms on the other side 3. factor dy/dx from each term 4. solve for dy/dx by dividing by the factor that does not contain dy/dx

Question 31

steps for logarithmic differentiation (used to simplify complicated exponents)

Answer 31

1. take the natural log of both sides of the equation 2. use log laws to simplify 3. differentiate implicitly with respect to x 4. solve for dy/dx

Question 32

what is the first derivative of a parametric function?

Answer 32

if x = f(t) and y = g(t) are differentiable with respect to t, then: dy/dx = (dy/dt) ÷ (dx/dt) in english: the derivative of y with respect to x equals the derivative of y with respect to t divided by the derivative of x with respect to t

Question 33

what is the second derivative of a parametric function?

Answer 33

if x = f(t) and y = g(t) are differentiable with respect to t, then: d²y/dx² = (d/dt)(dy/dx) ÷ (dx/dt) in english: the second derivative of y with respect to x equals the differential of the value dy/dx with respect to t divided by the derivative of x with respect to t note: this means that you must find the first derivative of the parametric in order to find the second derivative.