Chapter P Flashcards
Multiplying Conjugates

Difference of Two Squares

variable
a letter used to represent various Numbers
Special Products

Simplifying Exponential Expressions

Finding the Least Common Denominator

Adding and Subtracting Rational Expressions That Have Different Denominators

Factoring the Sum or Difference of Two Cubes

Finding nth Roots of Perfect nth Powers

Associative Property of Addition
Changing grouping when adding does not affect he sum.
(a + b) + c = a + (b + c)
Power Rule

Product to Powers

Simplifying Rational Expressions

Factoring Perfect Square Trinomials

Quotient to Powers

evaluating an algebraic expression
find the value of an expression for a given value of the variable
Definition of a1/n

Negative Exponents in Numerators and Denominators

Polynomial in x



set
a collection of objects whose contents can be clearly determined
Principal nth Root of a Real Number

Definition of am/n
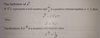
Quotient Rule

Product and Quotient Rules for nth Roots

roster method
the use of braces { } and commas to separate the elements of the set
Union of Sets
the set of elements that are membersof set A or of set B or of both sets. expressed as AUB

Properties of Negatives

Zero Exponent Rule

mathematical models
modeling formulas together with the meaning assigned to the variables
Converting from Decimal to Scientific Notation

Exponential Notation
a counting number raised to the nth power from a base number

Strategy for Factoring a Polynomial

Degree of axn

Important Subsets of the Real Numbers
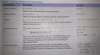
Order of Operations Agreement
Parenthesis - innermost to outermost Exponents Multiplications and divisions as they occur from left to right Additions and subtractions as they occur from left to right

Absolute Value

Absolute Value Properties
1
Product Rule

Subtraction and Division

Negative Exponent Rule

set-builder notation
the elements of the set are described but not listed (x,y)
Distance Between Two Points on a Number Line
|a - b| = |b-a|

elements
the objects in a set
equation
an equal sign is placed between two algebraic expressions
Multiplying Polynomials When Neither is a Monomial

Strategy for Factoring ax2 + bx + c

Properties of the Real Numbers
1
Product of the Sum and Difference of Two Terms

Irrational Numbers
the set of irrational numbers is the set of all numbers whose decimal representations are neither terminating nor repeating. Irrational numbers cannot be expressed as a quotient of integers.
Example:

algebraic expression
a combination of variables and numbers using the operations of addition, subtraction, multiplication, or division, as well as powers or roots
Whole Numbers
{0,1,2,3,4,5, … }
The set of whole numbers includes 0 and the natural numbers
Example: 0,2,3,5,17
Natural Numbers
{1,2,3,4,5,…} These are the numbers that we use for counting.
Example: 2,3,5,17
Using FOIL to Multiply Binomials

Product Rule for Square Roots

formula
an equation that uses variables to express a relationship between two or more quantities
Scientific Notation

Real Numbers
the set of numbers that are either reational or irrational

Intersection of Sets
the set of elements common to both sets A and B. expressed as

commutative property of multiplication
changing order when multiplying does not affect the product (ab = ba)
Example: x · 6 = 6x
mathematical model breakdown
when a mathematical model gives an estimate that is not a good approximation or is extended to include values of the variable that do not make sense.
mathematical modeling
the process of finding formulas to describe real-world phenomena
Square of a Binomial Sum

Quotient Rule for Square Roots

commutative property of addition
changing order when addeing does not affect the sum (a + b = b + a)
Example: 13+7=7+13
Rational Numbers
{a/b | a and b are integers and b<>0}
The set of rational numbers is the set of all numbers that can be expressed as a quotient of two integers, with the denominator not 0. Rational numbers can be expressed as terminating or repeating decimals.
Example: -17=(-17/1),-5=(-5/1),-3,-2,0,2,3,5,17,
(2/5)=0.4,(-2/3)=-0.6666
Square of a Binomial Difference

Integers
{…,-5,-4,-3,-2,-1,0,1,2,3,4,5,…}
The set of integers includes the negatives of the natural numbers and the whole numbers.
Example: -17,-5,-3,-2,0,2,3,5,17
Multiplying Rational Expressions

Principal Square Root



