Chapter 6 Terms Flashcards
-(x)y =?
-xy
-xy =?
-xy
(-x)y =?
xy
Ratio is usually written in _____ ______
Fraction form
Another name for quotient
Ratio
An equation with two equal ratios
Proportion
The quotient of two quatities
Ratio
A ratio in fact is no different from a ______ except that ratios are written using a notation other than fractional notation.
Fraction
1:2 & 1 to 2 is equal to?
1/2
what type of notation is this?—>1:4
Colon Notation
To write a ratio as a fraction you must…
1) Use the ratio’s first number as the Numerator
2) Use the ratio’s second number as the Denominator
Is this ratio (6 to 11) 11/6 or 6/11?
6/11
How to write a combo ratio. 2.6 to 3.1
2.6
_
3.1
How to write a combo ratio w/ mixed fractions. 1 1/2 to 7 3/4
1
1 -
2 \_ 3
7 -
4
To simplify ratio’s….
Make the ratio into a fraction and simply the fraction.
When simplifying ratios _____ ______ can be divided out as well _____ ______.
Common factors/ Common units
Because ratios are the quotient of two quantities the frational notation of a ratio is never written as a ____ ____. even if it is equal to the regular ______
Mixed fraction/ Fraction.
How do you clear the ratio of decimals?
Multiply the Ratio(that is in decimal notation) by power of ten so that the the decimal place moves accordingly.
- 6 x 100 = 260
- - - 15 x 100= 315
150
- = ..... 15000
* 150* 1
- = -
150 x 100 100
These are a special type of ratio
Rates
They are used to compare different kinds of quantities.
Rates
To simplify rates…
1) Find the GCF
2) Divide both the numerator and denominator by it
3) Your answer is the quotient.
* 3/33 *
* 3(gcf) x 1(other factor/answer) = 3 (given rate) *
* and *
* 3(gcf) x 11(other factor/answer)==33(given rate)*
Whenever you have different units for comparison in both the numerator and the denominator. You should ______ ______ _____ _____ in the numerator and denominator of both compared rates (fractions.)
Write the units out
The rates (fractions) with different units in the numerator and denominator DO NOT_____ _____
DIVIDE OUT.
A rate with a denominator of 1.
Unit rate
In the context of unit rates the word_____ translates in to division
Per
To make a rate a unit rate…
1) Divide the numerator by the denominator
2) Make the quotient the Numerator
3) Make “1” the denominator.
3600 ft 12 ft
- = -
300sec 1 sec
How to find unit prices…
1) Divide the numerator by the denominator
2) Make the quotient the Numerator
3) Make “1” the denominator.
4) Add the unit names
(number) Unit name
-
(number) Unit name
In economics a unit rate is also known as
Unit price
or
Money per item
or
Price per unit
You can use unit prices to determine the ____ _____
Better Buy
A statement that two ratios or rates are equal
Proportion
The rule of proportion
IF
A C
- & -
B D
are two ratios then
A C
- = -
B D is a proportion.
To emphasize a proportion we say…
A is to B as is C is to D
In two separate proportions the _______of one numerator must be the same as the other numerator. this also goes for the Denominator.
Unit.
The first way to compare to ratios to see if they are proportionate…
1) Write both in simplest form
2) Compare
3) If both are the same they are proportionate.
Ratio 1
(75/100) = 3/4
Ratio 2
(15/20)
Both ratios reduce to 3/4 thus they are proportionate.
The second way compare to ratios to see if they are proportionate…
1) Cross multiply the two ratios diagonally
2) If they both result in the same cross product they are proportionate.
The result of diagonally multiplying two ratios
Cross Product
To solve for x in two proportions…
1) Cross multiply
2) Place each cross product on separate sides of an equation
3) Solve for x
2/3 = x/30—-> 2*30=3*x
When two triangles have the same shape and the same size.
Congruence (Congruent)
If two angles have the same measure
Corresponding
Corresponding angles are marked the same way with a ____ ____.
Tic Mark

A straight line mark that intersects an arc used to denote the correspondence of angles in different/separate triangles.
or that intersects a side to denote the correspondence of side lengths in different/separate triangles.
Tic mark
The tic mark can also be used as a _____ tic, or ____tic as or none for the third side, as long as each corresponds to the side of both triangles.
Single/ Double
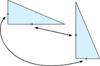
The rounded line that the tic intersects
An arc
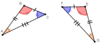
In congruent triangles the measures of corresponding angles are ______ and the length of corresponding sides are also ______
Equal
How to indicate angles with equal measure
∠ABC and ∠DEF
How to indicate sides with equal length
__ __
AB and CD
How to determine whether two triangles are congruent. A,S,A
1) If both triangles have two equal angles
and
2) The length between both pairs of equal angles is also equal.
How to determine whether two triangles are congruent. S,A,S
1) If both triangles have two equal sides
and
2) The angle between both pairs of equal sides is also equal.
How to determine whether two triangles are congruent. S,S,S
If both triangles have 3 equal lengths that correspond to each other.
When two triangles have the same shape but not necessarily the same size they are…
similar
In similar triangles the angles are ____
equal
In similar triangles the sides are_____
In proportion
What are the three ways to to prove congruencet???
Angle,Side,Angle
Side,Side,Side
Side, Side Angle
What is the one way not to determine congrunce?
Angle,Angle, Angle
What is the formula for a fulcrum balance.
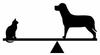
First Weight/ Second Distance= Second Weight/First Distance


