Chapter 4 Precalc Flashcards
Basic Sine Function

Basic Cosine Function

Degree to Radian Conversion
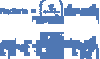
The Trigometric Functions

Adjacent, Hypotenuse, and Opposite Convert to
Adjacent=x
Hypotenuse=r
Opposite=y
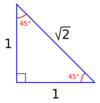
45 45 90
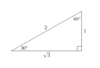
30 60 90
Where are trig functions positive?
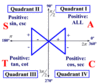
A positive angle goes
counterclockwise
A negative angle goes
clockwise
Trig functions of real numbers

Sinusoid Formula
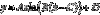
Amplitude of a Sinusoid
IaI
Period of a Sinusoid

Frequency of a Sinusoid

Phase shift of a sinusoid
phase shift=c
Tan Function

Unlike the sinusoids the tan function has a denominator
that might be zero, which makes the function undefined
tan x=
sin x/ cos x
the period of a tangent function is
π/ lbl
The Cotangent Function (reciprocal of the tangent function) and has asymptotes at zeros of the sine function

The Secant Function (Reciprocal of the cosine function)

The Cosecant Function (reciprocal of the sine function)
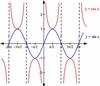
for the sum to be a sinusoid the periods of two sinusoids to be added together must be
the same and the sum must have the same sum



