Chapter 4, 5 Flashcards
Probability Mass Function
Same as “probability distribution” The relationship between the (quantity) values of a random variable X and each of their associated probabilities.
Sum of probabilities of all possible events = 1
Probability is between 0 and 1
Combination
- Number of ways of selecting k objects out of n
- Order of selection MATTERS

Permutation
- The number of ways of selecting k objects out of n
- Order of selection MATTERS
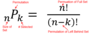
Binomial Distribution Formula
- For statistically independent trials
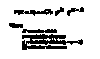
Expected Value of a Binomial Distribution
E(x) = np
Variance of a Binomial Distribution
Var (X) = npq
The Poisson Distribution
- Associated with rare events

Expected Value and Varience of
The Poisson Distribution
The mean and variance both = µ
E(X) = λT = Var(X) = λT = μ
Poisson Approximation to the
Binomial Distribution
The binomial distribution with large n and small p can be accurately appoximated by a Poisson distribution with parameter µ = np
Probability Density Function
Function such that the area (integral) under the density-function curve between any two points is equal to the probability that the random variable X falls between the two points
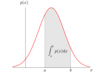
Cumulative Density Function
Gives the probability (area under the curve) between
-∞ to some value X
Variance of a continuous random variable
Variance of a continuous random variable X is the average squared distance of each value from the mean
Expected value E(X)
of a continuous random variable
The average value taken on by the random variable
Standard Normal Distribution
Normal distribution with mean 0 and variance 1
N(μ,σ2) = (N(0,1)
In a continuous probability distribution, the probability of a single value is ____.
Zero (0)


