Chapter 4 Flashcards
What is parameter learning / parametric modelling?
A model specified by a data miner is finetuned through the use of data mining so that the model fits the data as well as possible.
Most common examples: linear models, such as linear regression
What are some of the assumptions made in this chapter?
- First, for classification and class probability estimation we will consider only binary classes: the models predict events that either take place or do not, such as responding to an offer, leaving the company, being defrauded, etc. The methods here can all be generalized to work with multiple (nonbinary) classes, but the generalization complicates the description unnecessarily.
- Second, because we’re dealing with equations, this chapter assumes all attributes are numeric. There are techniques for converting categorical (symbolic) attributes into numerical values for use with these equations.
- Finally, we ignore the need to normalize numeric measurements to a common scale. Attributes such as Age and Income have vastly different ranges and they are usually normalized to a common scale to help with model interpretability, as well as other things (to be discussed later). We ignore these complications in this chapter. However, dealing with them is ultimately important and often necessary regardless of the data mining technique.
What are linear discriminant functions?
- A type of multivariate supervised segmentation
- Discriminates between the classes
- The function of the decision boundary is a linear combination (a weighted sum) of the attributes
- A numeric classification model
- When there are only two-dimensions, the discriminant is a line; in three dimensions a plane, +3 dimensions a hyperplane
- Provide a ranking of cases by the likelihood of belonging to one class or another.
What is a parameterised model?
- The weights of the linear function are the parameters
- Data mining fits the parameterized model to a particular dataset
- The larger the magnitude of a feature’s weight, the more important that feature is for classifying the target
I feel like these are the fundamentals that data mining tasks use.
What are Objective functions?
- A function that represents the goal and can be calculated for a particular set of weights and a particular set of data
- Finding the optimal values for the weights by maximizing or minimizing the objective function
- Note: Weights only work in our favor if the objective function actually represents what we aim to achieve
What are SVMs? How do you find the best linear discriminant?
- A type of linear discriminant
- Classifies instances based on a linear function of the features (line that separates).
- Goal: find a linear discriminant/ center line with the largest margin
- How to find the best linear discriminant?
- Start with fitting the fattest bar possible between the classes
- The wider the bar, the better
-
Center of the bar is the linear discriminant, with the largest margin possible
- Margin: the distance between the border of the bar and the center line
- Maximum margin: most leeway possible, e.g. margin for error
-
SVMs penalize a training observation for being on the “wrong” side of the decision boundary.
- If the data are not linearly separable, the best fit is some balance between a fat margin and a low total error penalty.
- The penalty function used is commonly known as Hinge Loss
- the penalty for a misclassified point is proportional to the distance from the decision boundary
- Start with fitting the fattest bar possible between the classes

What are Loss Functions and which ones should you know?
- A loss function determines how much penalty should be assigned to an instance based on the error in the model’s predicted value.
-
SVM - Hinge Loss
- No penalty for correctly classified example / instance
- Penalty for wrongly classified instance
- Loss increases linearly form the margin with further distance
- Large errors are more penalized
-
Zero-one-loss
- No loss for wrong decision
- One point for a falsely classified instance
-
Squared error
- Specifies a loss proportional to the square of the distance from the boundary
- Used for numeric value prediction (regression), rather than classification
- Would also penalize instances that are on the correct side, but far from the center line
Fitting linear functions to regression
- The common “standard” linear regression model is a powerful and convenient choice for an objective function
- Intuitive notion of the fit of the model: How far away are the predicted values (by the model) from the true values on the training data? Or how large is the error of the fitted model?
- The linear regression model structure is exactly the same as for the linear discriminant function.
- Many different objective functions for linear regression to optimise models fit to data.
- Regression problems: target variable is numeric
- Choose the best regression: sum up all the errors (one way or the other) for all data points and choose the model with the lowest minimum sum of errors
- Standard linear regression procedures minimize the sum or mean of the squares of the errors
- Any choice for the objective function has advantages and drawbacks
- Least squares regression: very sensitive to the data, e.g. outliers can severely skew the resultant linear function. Only the objective function determines if penalizing is appropriate
What’s the difference between odds and probability?
Odds is the ratio between something happening (i.e. winning) and something not happening (i.e. losing).
Probability is the ratio between something happnening and everything that could happen (i.e. winning and losing)
Why is log often applied to odds?
To normalise the magnitude differences between odds greater than 1 going to infinity and odds between 0 and 1. Since log looks at the exponent, it makes everything symmetrical and make it easy to compare.
What is the Odds ratio?
The odds ratio is the ratio of the odds of an event occurring in one group to the odds of it occurring in another group.
For example, say you’re comparing the association between a mutated gene and cancer, and you have a confusion matrix. A large odds ratio indicates that the gene is a good predictor of cancer. Conversely, a small value indicates that it isn’t a good predictor.
What is logistic regression?
Logistic regression is a model/method that has an objective function designed to give accurate estimates of class probability.
Logistic regression uses the same linear model as linear discriminants for classification and linear regression for estimating numeric target values.
Output of Logistic regression is interpreted as the log-odds of class membership. This can directly be converted to probability of class membership
What is the logistic function?
Where f(x) is the linear function.
The model is fitted by determining the slope of the almost-linear part and thererby how quickly we are certain of the class as we move away from the boundary.
p+ is the class that we are trying to model
p+ should be as close as possible to 1 for positive instances
p+ should be as close as possible to 0 for negative instances
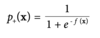
What is the objective function generally used by Logistic regression?
- Logistic models are estimated using maximum likelihood estimation
- The set of weights in the objective function on average give the:
- Highest probabilities to the positive examples
- Lowest probabilities to the negative examples
For Linear Discriminant, Linear regression and Logistic regression what do each estimate/predict and what is the target variable type?

What does the linear part of the Logistic regressions estimate tell us?
The slope of the almost-linear part tells us how quickly we are certain of the class as we move away from the line.
How would you choose between Decision Trees and Logistic regression?
Which model is more appropriate depends on the background of the stakeholders (i.e. statistical knowledge, making it easier to understand logistic regression).
What is the similarity between Decision Trees and Logistic regression and what are the key differences?
Similarity: classification trees and linear classifiers both use linear decision boundaries.

What are the most common techniques that are based on fitting the parameters of complex, non-linear functions?
What are the disadvantages?
Nonlinear support vector machines and Neural networks
Support vector machines have a so-called “kernel function” that maps the original features to some other feature space
Neural networks implement complex nonlinear functions as a “stack” of models, where the results of the previous model are used as input to the next model
Target labels for training are generally only provided for the final layer (the actual target variable)
Disadvantage:
- Due to the increased flexibility of fitting the data, there is a risk of fitting the data too well (overfitting)
- Finding patterns that specifically apply to the training data instead of the general population, for whom we are building the model
How you can apply logistic regression for the case that your explanatory (or input) data has categorical variables?
To perform logistic regression the variables need to be numeric. If the input data is categorical, it would be converted into numeric using dummy variables. In the case that the categorical values are binary, 0 and 1 can be used. If they are not binary, the different levels can be defined by more complex 0 and 1 combinations.
What effect does a moving point have on the maximal margin classifier? What would happen with logistic regression?
It shouldn’t change anything about the maximal margin classifier unless it moves within the margin maximising boundary, then it could change the margin, it would shrink it for example depending on the tradeoff between error and margin size. If it moves to the other side of the boundary then the SVM either crashes or consider it an error. You can adjust this by giving how many possible errors it can accept.
Logistic regression would adapt since it is sensitive to al points.
What is the purpose of the kernel approach in a support vector machine? How does changing the kernel changes the location of the decision boundary?
The kernel approach allows you to apply SVM in cases where we cannot find a straight line, i.e. we apply SVM non-linearly. The kernel function allows you to map the original features to another feature space (i.e. x-y coordinates). In other words, when the dataset is inseparable in the current dimension, add another one. The rule is usually to go one dimension up.
Changing the kernel will vary how the decision boundary is drawn. As the dimensions increase the decision boundaries can become increasingly complex.


