Chapter 4 Flashcards
infinite sequence [definition]
a list of intergers xj for j ∈ N, denoted (xj)∞j=m
finite sequence [definition]
a list of numbers xm, xm+1, xm+2,…,xM-1, xM ;
denoted (xj)Mj=m , where M ∈ Z with m ≤ M

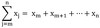

(note: if m = n, this is interpreted as )
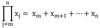
definition of n! (“n factorial”) [definition]

[finite series]
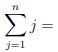
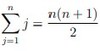
[finite series]
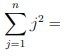
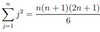
[finite series]

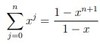
[finite series]
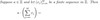

[finite series]
if a ∈ Z, then for all n ∈ N,
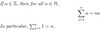
[finite series]

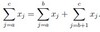
[finite series]


[finite series]

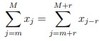
[finite series]
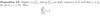

binomial theorem [theorem]
Suppose k, m ∈ Z≥0, with m ≤ k.
Then k! is divisible by m!(k-m)! .
[theorem / formula]
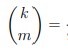
“k choose m”
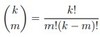
binomial theorem for intergers [theorem / formula]
If, a, b ∈ Z and k ∈ Z≥0, then

[corollary] for k ∈ Z≥0, we have

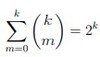
Principle of mathematical induction—second form (“strong induction” [theorem]
For each k ∈ N, let P(k) be a statement. Assume that:
- P(1) is true, and
- if P(j) is true for all integers j such that 1 ≤ j ≤ n, then P(n + 1) is true.
Then P(k) is true for all k ∈ N.


