Chapter 3: Managing Portfolios (Theory)

Question 1

Covariance

Answer 1

Measures the co-movement or co-variability of two variables. Example: the covariance of two assets’ returns is an index of how they tend to move relative to each other.

Negative covariance = best diversification

Close-to-zero Covariance = good diversification

High-positive Covariance = poor diversification

Question 2

Correlation Coefficient

Answer 2

Since the covariance statistic is difficult to interpret because of the ambiguity of its units and interpretation of its magnitude, the correlation coefficient is a better measurement of co-movement. It is defined as the covariance divided by the product of the standard deviations.

Question 3

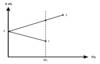
Efficient Frontier

Answer 3

A set of portfolios, each of which offers the highest expected return for a given risk and the smallest risk for a given expected return.

The “upper line segment” in the figure below.

Question 4

Utility Functions

Answer 4

A utility function for wealth reflects the value (or utility) of incremental wealth to a particular individual.

Example: $1,000 with perfect certainty versus 50/50 chance of receiving $2,000 or nothing at all. Most people would prefer the $1,000 with perfect certanty.

Question 5

Indifference Curves

Answer 5

Derived from utility functions, an indifference curve is a locus of portfolios among which an investor is indifferent (doesn’t matter).

Question 6

Separation Theorem

Answer 6

An investor’s risk preferences do not affect his or her choice of risky assets, because M is the only rational choice.

Question 7

Market Portfolio

Answer 7

The portfolio of all assets, with the weight of each based on its market value.

Question 8

Capital Market Line

Answer 8

The line formed by the risk-free asset and the market portfolio.

Question 9

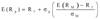
Capital Asset Pricing Model (CAPM)

Answer 9

The theoretical model that seeks to explain returns as a function of the relationship between the risk-free rate, market risk premium, and beta.

Question 10

Beta

Answer 10

Also known as beta coefficient or beta statistic. A parameter in the CAPM and APM models that relates stock or porfolio performance to market performance.

Example: with x percent change in market, stock or portfolio will tend to change by x percent times its beta

Question 11

Security Market Line (SML)

Answer 11

The theoretical relationship between a security’s market risk and its expected return under the capital asset pricing model.

r_i = r_f + ß_i (r_m r_f)

Question 12

Index Model Characteristic Line

Answer 12

A regression of an asset’s excess returns against the market’s excess returns.

Question 13

Coefficient of Determination

Answer 13

(R²)

A measure of how well the regression line (characteristic line) fist the data.

Question 14

Nonmarket Risk

Answer 14

Risk not related to general market movements. This risk is diversifiable.

Question 15

Arbitrage Pricing Theory (APT)

Answer 15

A model used to explain stock pricing and exprected return that introduces more than one factor in place of (or in addition to) the capital asset pricing model’s market index.

Question 16

Uniform Principal and Income Act of 1931

Answer 16

The original law affecting the management of trust assets. Laid out the principle known as the Prudent Man Rule.

Question 17

Prudent Man Rule

Answer 17

This rule states that each security or asset in a trust must meet this standard: It must be one in which a prudent man who wanted first and foremost to ensure the presearvation of his assets would invest.

Question 18

Prudent Investor

Answer 18

A revision to the Prudent Man Rule, this rule states the the trustee must act as a prudent investor, rather than a prudent man (the investor can invest using the principles of modern portfolio theory).