Chapter 2 Descriptive Statistics

Question 1

Percentile

Answer 1

Percentile – a data point’s percentile is the percentage of the data smaller than or equal to it. data is ordered.

Question 2

Stem and Leaf Graphs

Answer 2

Stem and Leaf Graphs (Stem plots) - Comes from the field of exploratory data analysis It is a good choice when the data sets are small.

Question 3

Line graph

Answer 3

Question 4

Bar Graph

Answer 4

Question 5

Histogram

Answer 5

Histogram - A histogram has both a horizontal axis and a vertical axis. The horizontal axis is labeled with what the data represents (for instance, distance from your home to school). The vertical axis is labeled either Frequency or relative frequency.

EXAMPLE

The following data are the number of books bought by 50 part-time students in SCSU. The number of books is discrete data since books are counted.

1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1

2; 2; 2; 2; 2; 2; 2; 2; 2; 2

3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3; 3

4; 4; 4; 4; 4; 4

5; 5; 5; 5; 5

6; 6

Eleven students buy 1 book. Ten students buy 2 books. Sixteen students buy 3 books. Six students buy 4 books. Five students buy 5 books. Two students buy 6 books.

Question 6

Boxplots

Answer 6

Boxplots - give a good graphical image of the concentration of the data. They also show how far from most of the data the extreme values are. The box plot is constructed from five values: the smallest value, the first quartile, the median, the third quartile, and the largest value.

Question 7

Quartiles

Answer 7

Quartiles - are numbers that separate the data into quarters. Quartiles may or may not be part of the data.

Q1 = 25^th percentile

Even: 1,2,3,4,5,6,7,8

[1,2]Q1[3,4],[5,6,7,8

Q1 = (2+3)/2 = 2.5

Odd: 1,2,3,4,5,6,7,8,9

(.25)*(number of data) = (.25)*(9)=2.25(round up) = 3

Q1 = 3^rd item on the list , which is 3

Q2 = 50^th percentile = median

Q3 = 75^th percentile

Even: 1,2,3,4,5,6,7,8

[1,2],[3,4],[5,6]Q37,8

Q3 = (6+7)/2 = 6.5

Odd: 1,2,3,4,5,6,7,8,9

(.25) *(number of data) = (.75) *(9) =6.75(round up) = 7

Q3 = 7^rd item on the list, which is 7

Q4=100^th percentile = maximum value

Question 8

Median

Answer 8

Median: A number that separates ordered data into halves.

Question 9

Boxplot Example

1; 1; 2; 2; 4; 6; 6.8; 7.2; 8; 8.3; 9; 10; 10; 11.5

Answer 9

Question 10

Interquartile Range

Answer 10

Interquartile Range ^is IQR=Q3−Q1

The IQR can help to determine potential outliers. A value is suspected to be a potential outlier if it is

• less than 1.5*IQR below the first quartile

or

• more than 1.5*IQR above the third quartile

Question 11

Mean

Answer 11

Mean: A common name for mean is ‘average

Question 12

Mode

Answer 12

Mode: The value that appears most frequently in a set of data

Ex.

1,2,3,4,5: No mode

1,1,2,3,4: Mode is 1 unimodal

1,1,2,2,3: Mode is 1 & 2 bimodal

1,1,2,2,3,3,4: Mode is 1 , 2, & 3 multimodal

Question 13

symmetrical distribution

Answer 13

symmetrical distribution - In a perfectly symmetrical distribution, the mean and the median are the same.

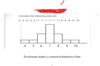
Mean = Median = Mode

Question 14

skewed to the left

Answer 14

skewed to the left - is not symmetrical. The right-hand side seems “chopped off” compared to the left side. The shape distribution is called skewed to the left because it is pulled out to the left.

Question 15

skewed to the right

Answer 15

skewed to the right - is not symmetrical. The left-hand side seems “chopped off” compared to the right side. The shape distribution is called skewed to the right because it is pulled out to the right.

Question 16

standard deviation

Answer 16

standard deviation - is a number that measures how far data values are from their mean. It’s basically the is the “average” difference between the data points and the average of those data points.

Question 17

Standard Deviation symbol for sample vs population

Answer 17

S = sample’s std

σ = population std

Question 18

How to Find standard deviation?

Answer 18

Question 19

Variance

Answer 19

Variance – square of the standard deviation