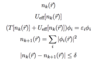Chapter 12: Quantum Calculations Flashcards
1
Q
Hamiltonian under Born-Oppenheimer Approximation
A
- can separate and decouple nuclear and electronic wavefunctions

2
Q
Hartree Method
(Assumptions)
A
- non-interacting electrons
3
Q
Hartree Wavefunction
A
-
Drawbacks:
- not antisymmetric → no exchange
- only include Coulomb correlation
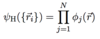
4
Q
Hartree Single Particle Equation
A
- gives energy and orbital for electron i

5
Q
Hartree-Fock Wavefunction
A
- uses Slater determinant to form wavefunction
- includes Pauli Principle exchange
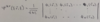
6
Q
Hartree-Fock Single Particle Equation
A
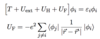
7
Q
Hartree-Fock Approximations
A
- Born-Oppenheimer
- Coulomb correlation only
- non-relativistic
- attainable phase space is constrained by single Slater determinant
8
Q
Post-HF Methods
A
- mostly aim to increase correlation
- may try to increase phase space
- e.g. Coupled-Cluster Method
9
Q
Coupled-Cluster Method
A
- can look at excited states
- good for chemical reactions with small molecules
- increases correlation

10
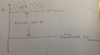
Q
Hartree-Fock Limit
A
- HF groundstate prediction be bounded by below and is an overestimate for true groudstate
11
Q
Density Functional Theory
A
Reduces 3N-dimensional wavefunction to 3-dimensional wavefunction using density n(r )
12
Q
Hohenberg-Kohn Theorems
A
- There exists a one-to-one mapping between groundstates density and groundstate wavefunction for non-degenerate groundstates
- Groundstate density minimizes total energy.
13
Q
Kohn-Sham Equation
A
- ε<em>i</em>, φi are for fictitious particle i
- however, densities match nDFT(r ) = nexact(r )
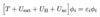
14
Q
Exchange-Correlation Functional
A

15
Q
Local Density Approximation
A
- local functional
- uses homogeneous electron gas exchange-correlation
- fails for vdW forces and metallic systems
16
Q
Generalized Gradient Apprixmation
A
- semi-local functional
- also depends on gradient of density

17
Q
DFT Short-Comings
A
- overbinding → underestimates bandgap
- can only predict trends for excited states → TDDFT better for excited states
18
Q
Time-Dependent DFT
A
- rewrite KS equations in time-dependent manner using quantum mechanical action A[n]
- need new functionals because (non-)locality can occur in space and time
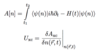
19
Q
Pseudo-Potentials
A
Used to neglect core electrons and avoid singularities
- functional specific
20
Q
DFT Algorithm
A
- Initial guess of density
- Evaluate potential
- Solve KS equation
- Get new density
- Test for self-consistency