Chapter 12 - Data-Based and Statistical Reasoning Flashcards
Measures of central tendency:
measurements that describe the middle of a sample
Outlier:
an extremely large or extremely small value compared to the other values
Median:
- what it is also known as
- relationship to outliers
- if mean and median are far from each other
- if mean and median are very close
- equation
- Midpoint; where half of data points are greater than the value and half are smaller
- Least susceptible to outliers, but not useful for data sets with very large ranges or multiple modes
- If the mean and median are far from each other, implies the presence of outliers or a skewed distribution
- If the mean and median are very close, this implies a symmetrical distribution
Mode:
- what it is
- if a data set has two modes
- Number that appears the most often in a set of data
- If a data set has two modes with a small number of values between them, it may be useful to analyze these portions separately or to look for other variables that may be responsible for dividing the distribution into two parts
Normal Distributions:
- what is all the same
- basis for what
- All of the measures of central tendency are the same
* We can transform any normal distribution to a standard distribution, with a mean of zero and a standard deviation of one* - Basis for the bell curve
Skewed Distribution:
- what they are
- negatively skewed distribution
- where tail is
- mean and median relationship
- positively skewed distribution
- where tail is
- mean and median relationship
1. Skewed distribution: one that contains a tail on one side or the other of the data set
- Negatively skewed distribution
- Tail on the left (or negative) side
- Mean will be lower than the median
- Positively skewed distribution
- Tail on the right (or positive) side
- Mean will be higher than the median
(in image: a = negative, b = positive)
Bimodal Distributions:
Bimodal: a distribution containing two peaks with a valley in between
May only have one mode if one peak is slightly higher than the other
Range:
- what it is
- does not consider what
- relationship to outliers
- relationship to standard deviation
- equation
- difference between its largest and smallest values
- Does not consider the number of items of the data set
- Heavily affected by the presence of outliers
- Possible to approximate the standard deviation as one-fourth of the range
- Range = xmax − xmin
Interquartile range + Quartiles:
- what they are
- equation for IQR
Interquartile range: related to the median, first, and third quartiles
Quartiles: including the median (Q2), divide data into groups that comprise one-fourth of the entire set
- The interquartile range is then calculated by subtracting the value of the first quartile from the value of the third quartile:
IQR = Q3 – Q1
Standard Deviation:
- can be used to determine what
- what determines an outlier
- on a normal distribution
- one standard deviation
- two standard deviations
- three standard deviations
- Can be used to determine whether a data point is an outlier
2. If a data point falls more than three standard deviations from the mean, it is considered an outlier
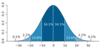
- On a normal distribution:
- 68% of data points fall within one standard deviation of the mean
- 95% fall within two standard deviations
- 99% fall within three standard deviations
Reasons why outliers occur: (3)
- A true statistical anomaly (ex: a person who is over seven feet tall)
- A measurement errors (ex: reading the centimeter side of a tape measure instead of inches)
- A distribution that is not approximated by the normal distribution (ex: a skewed distribution with a long tail)
Independent events vs. Dependent events:
Independent events: have no effect on one another
ex: rolling a dice, picking it up, and rolling it again
Dependent events: do have an impact on one another, such that the order changes the probability
ex: container with five red balls and five blue balls, if you pick up one and don’t put it back, probability changes
Mutually exclusive outcomes:
cannot occur at the same time
Ex: Cannot flip both heads and tails in one throw
Exhaustive (when describing a group):
describes a group when there are no possible outcomes
Ex: flipping heads or tails are exhaustive outcomes of a coin flip; these are the only two possibilities
Null hypothesis (H0):
a general statement or default position that there is no relationship between two measured phenomena, or no association among groups
the hypothesis that there is no significant difference between specified populations, any observed difference being due to sampling or experimental error
Says that two populations are equal, or that a single population can be described by a parameter equal to a given value
Assumed to be true until evidence indicates otherwise
Alternative Hypothesis:
- Nondirectional
- Directional
Alternative hypothesis: may be nondirectional or directional
Nondirectional: that the populations are not equal
Directional: ex - the mean of population A is greater than the mean of population B
Test statistic:
- what it is
- what is also called
- calculated and compared to a table to determine the likelihood that the statistic was obtained by random chance (under the assumption that our null hypothesis is true)
2. This is the p-value
P-value is compared to what?
when it’s greater
when it’s less
a significance level (α); 0.05 is commonly used
If p-value is greater than α, then we fail to reject the null hypothesis
If p-value is less than α, then we reject the null hypothesis and state that there is a statistically significant difference between the two groups
When the null hypothesis is rejected…
we state that our results are significantly significant
Type I error & Type II error:
(Type II error - symbolized by what)
Type I error: likelihood that we report a difference between two populations when one does not actually exist
Type II error: occurs when we incorrectly fail to reject the null hypothesis
Likelihood that we report no difference between two populations when one actually exists
Symbolized by β
Power:
the probability of correctly rejecting a false null hypothesis (reporting a difference between two populations when one actually exists)
Equal to 1 - β
Confidence:
the probability of correctly failing to reject a true null hypothesis (reporting no difference between two populations when one does not exist)
Confidence intervals:
reverse of hypothesis testing
We determine a range of values from the sample mean and standard deviation
We begin with a desired confidence level (95% is standard) and use a table to find its corresponding z or t score
Example: consider a population for which we wish to know the mean age. We draw a sample from that population and find that the mean of the sample is 30, with a standard deviation of 3. if we wish to have 95% confidence, the corresponding z-score (which would be provided on test day) Is 1.96.
- Thus the range is 30-3(1.96) to 30+(3)(1.96) = 24.12 to 35.88
- We can report that we are 95% confident that the mean age of the population from which this sample is drawn is between 24.12 and 35.88.
Slope:
change in the y-direction divided by the change in the x-direction for any two points:
Semilog graphs:
specialized representation of a logarithmic data set
They can be easier to interpret because the curved nature of the logarithmic data is made linear by a change in the axis ratio
One axis (usually x-axis) maintains the traditional unit spacing
Correlation:
- what it is
- relationship to causation
- if an experiment cannot be performed
- refers to a connection - direct relationship, inverse relationship, or otherwise - between data
- Correlation does not imply causation
- If an experiment cannot be performed, we must rely on Hill’s criteria
