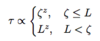Chapter 11: Observables in Phase Transition

Question 1

First-Order Phase Transition

Answer 1

discontinuity in the order parameter

Question 2

Second-Order Phase Transition

Answer 2

• critical singularity can be described by critical exponent with respect to t = |1 - T/T_C|
  
  • universality class: important here; relevant parameters
    
    • spatial dimensionality D
    • symmetry of order parameter

Question 3

Specific Heat, Magnetization, and Magnetic Susceptibility

Answer 3

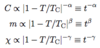
Question 4

Correlation Function

Answer 4

• correlation length diverges as T → T_C
  
  • details of lattice and short-range behavior become irrelavant → reason for universality

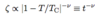
Question 5

Scaling and Hyperscaling

Answer 5

• there exist only 2 independent critical exponents
  
  • there exist scaling relationships between critical exponents

Question 6

Finite-Size Scaling Theory

(Overview)

Answer 6

• L finite → Z is infinitely differentiable analytic power series → no singularities possible
• maxima are rounded and displaced
  
  • max{ζ} ~= L

Question 7

Finite-Size Scaling Theory

(Assumptions)

Answer 7

• consider susceptibility (below)
• actually measure scaling function in simulation
  
  • should get same results regardless of choice of L
  • allows for extrapolation of γ/ν, 1/ν, T_c

Question 8

Critical Slowing-Down

Answer 8

• correlation time τ for loval MC algorithm given below
  
  • Recall: N_eff = N/(2τ)
  • as L increases, τ increases faster, meaning much longer time is needed to each the same level of accuracy
• can overcome by using clust algorithms (e.g. Wolff algorithm)