Chapter 1 Concepts plus regression review Flashcards
Three principles of design:
- replication
- randomization
- local control of error (blocking)
Categories of experimental problems
- Treatment comparisons
- Variable screening
- Response surface exploration
- System optimization
- System robustness
Steps to experiment planning
- State objective
- Choose response
- Choose factor and levels
- Choose experimental plan
- Perform experiment
- Analyze the data
- Draw conclusions and make recommendations
Experimental units vs observational units
- Experimental unit is item that is being experimented on and measured
- Observational unit can be thought of as a technical replicate
Replication does the following:
- Replicating experimental units:
- Allows estimation of the experimental error
- Improves the precision of the estimates
- Replicating observational units:
- mimizes the impact of measurement error
- does NOT estimate experiment error
Randomization does the following
- Distributes the impact of any systematic bias
- ensures fair comparisons
- if bias is present, inflatest the estimate of error
- Elimates presumption bias
Local control of error does the following
- Also called blocking
- reduces the random error among the experimental units
- controls for anything which might affect the response other than the factors
Two important forms of local control of error:
- blocking
- covariates
Block
Groups of homogeneous units
Blocking
- arranged so that within block variation is smaller than between block
- should be applied to remove the block-to-block variation
- randomization is applied to assignments of treatments within the blocks
Derive the LSE estimators without matrix notation
Derive the LSE estimators using matrix notation
(X’X)-1X’y
Derive the expectation, variance and covariance estimates of the LSE estimators without using matrix notation
Derive the expectation, variance, and covariance of the LSE estimators using matrix notation
How do you estimate σ2 in LSE
σ_hat2 =
MSE =
RSS/(N-k-1)=
SUM (yi - yi_hat)2 / (N-k-1)
yT(I-H)y / (N-k-1)
For SLR, N-k-1 = N-2
degrees of freedom in multiple linear regression
df overall = N-1
df model = k
df error = N-k-1
Note: this assumes k regressors + intercept
such that model matrix is n x k+1
standard error beta1_hat
=sqrt(MSE/Sxx)
SST =
SST = SSReg + SSRes
R2 = (in SS components)
R2 = SSreg/SST = 1 - SSres/SST
R2 = (Pearson format)
R2 = SxySxy / SxxSyy
ANOVA style F stat for MLE
F = (MSReg/df1) / (MSres/df2)
where df1 = difference in full and reduced model parameters
df2 = total df - number of parameters in full model
Confidence interval for beta1_hat in SLR
beta1_hat +/- tn-2,alpha/2 * se(beta1_hat)
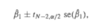
Confidence/prediction interval for y_hat( at x0)
CI: y_hatxo = tN-2,alpha/2 * sqrt(MSres) * sqrt(1/N + (X_bar - Xo)2/Sxx)
PI: y_hatxo = tN-2,alpha/2 * sqrt(MSres) * sqrt(1+ 1/N + (X_bar - Xo)2/Sxx)
Extra sum of squares principle
- Two models: Model I (reduced) and Model II (full)
- Model I is a sub-model of Model II
- F stat = (SSred - SSfull)/(q-k) /
- (SSfull/df_full)
R2, Ra2, and Cp (SS’s)
R2 = 1 - SSres/SST
Ra2 = 1 - MSreg / SST/df_total
Cp = SSres/MSE - (N-2p)
AIC and BIC
AIC = N ln (SSres/N) + 2p
BIC = N ln (SSres/N) + p ln (N)
Model selection methods
Forward selection
Backwards elemination
Stepwise
Best subsets
E(Cp) =
If model is true, E(RSS) = (N-p)σ2
E(Cp) = (N-p)σ2/σ2 - (N-2p)
=p
MLR CI for beta_hatj
beta_hatj +/- tN-k-1, alpha/2 * sqrt ( MSE * (X’X)-1jj )
MLR contrast
aTbeta ~ ( , ) and
test stat
