Chapter 1

Question 1

the Least Upper Bound Axiom

Answer 1

Completeness Axiom

Rationals= {a/b: a,b are Integers and b=/=0}

Every non-empty subset of R that is bounded above has a supremum

Question 2

the supremum of a non-empty set K ⊆ R

Answer 2

Let K⊆R and let x be an element of R.

x is a _________ for k if :

a) x is an upper bound for k
b) y is an upper bound for k, then x is less than or equal to y

Question 3

Archimedean Property

Answer 3

For all x in R, there exists an n in N st n>x

The natural numbers are unbounded

Question 4

a countable set

Answer 4

an infinite set A is _______ if there exists a bijection f:N→A

The natural numbers are countable

Question 5

metric space

Answer 5

a place where there is a notion of distance. Let X be a set and let d: X * X→ R⁺ st

1. d(x,y) is greater than or equal to 0
2. d(x,y) = d(y,x)
3. d(x,y) = 0 ⇔ x=y
4. d(x,z) is less than or equal to d(x,y)+d(y,z) for all x, y, and z in X

d is a metric on X and (X,d) is a ________

Question 6

the Euclidean Metric on Rⁿ

Answer 6

Let n be a natural number and consider the “generalized Euclidean space,” Rⁿ. We define the usual metric d : Rⁿ × Rⁿ → R on Rⁿ as follows. For two points (x₁, …, x_n) and (y₁,…, y_n) in Rⁿ, define

Question 7

The Cauchy-Schwarz Inequality Theorem

Answer 7

For all x = (x₁, . . . , x_n) and y = (y₁, . . . , y_n) in Rⁿ,

Question 8

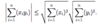
Let K⊆R and let x be an element of R.

x is an ______ _______ for k if x is greater than or equal to k for all k in K

Answer 8

upper bound

Question 8

Theorem 1.4.4 about non-empty subsets of R bounded above. Let b be an upper bound for B. TFAE:

Answer 8

1. b= supB
2. For all epsilon positive there exists an x in B s.t

|x-b| < epsilon

3. for all epsilon positive there exists an x in the intersection of B and (b-epsilon, b]

Question 9

Corollary of the Archimedean Property

Answer 9

For all epsilon positive, there exists an n in N st 1/n < epsilon

Question 10

Theorem 1.4.8 (Proof requires LUBA)

Answer 10

For all a in the positive R there exists an x in R st x²=a

Question 11

Corollary from 1.4.8

Answer 11

There exists an irrational

Question 12

Nested Interval Theorem

Answer 12

Every nested sequence of non-empty, closed intervals has non-empty intersection.

If (a_n) and (b_n) are sequences s.t.

1. a_nn for all n
2. for all n a_n is less than or equal to a_n+1 and b_n is less than or equal to b_n+1

_​then the infinite intersection of [a_n,b_n] is non-empty

Question 13

The reals are ___ ________

Answer 13

not countable

Question 14

bounded set

Answer 14

A set S of real numbers is called bounded from above if there is a real number k such that k ≥ s for all s in S. The number k is called an upperbound of S. The terms bounded from below and lower bound are similarly defined. A set S is bounded if it has both upper and lower bounds