Ch 5: Handy Circuit Analysis Techniques

Question 1

Handy Circuit Analysis Techniques and Principles

covered in this chapter

Answer 1

Superposition

Source Transformation

Thévenin Equivalent Circuit

Norton Equivalent Circuit

Maximum Power Transfer Theorem

Delta-Wye Equivalents

Question 2

Linear Circuit:

Definition

Answer 2

A circuit composed entirely of:

• Independent Sources
• Linear Dependent Sources
• Linear Elements

Question 3

Linear Element:

Definition

Answer 3

A passive element that has a linear voltage-current relationship

Question 4

Superposition:

Basic Idea

Answer 4

Remove all independent sources.

Then, apply one source at a time, calculating the resulting voltage or current values.

Finally, add the results together.

*Only applies to linear circuits.

Question 5

Superposition:

Steps

Answer 5

1. Turn off all independent sources except one. Find the output voltage or current due to that source
2. Repeat for each independent source
3. Find the total contribution by summing all the contributions due to the independent sources

Question 6

Principle of

Superposition

Answer 6

The total response(desired current or voltage) of a Linear Circuit with multiple independent sources can be obtained by summing the responses caused by the separate independent sources.

Question 7

Superposition:

How to turn off an Independent Current Source

Answer 7

Simply remove the source, replacing it with an open circuit.

Question 8

Superposition:

How to turn off a Voltage Source

Answer 8

Take out the source, connect the two terminals.

Replaces the Voltage Source with a short circuit.

Question 9

Practical Current Source

Answer 9

A current source model that more closely matches real world sources.

Represents the internal resistance inherent in a current source by placing a very resistance in parallel with an ideal current source.

Question 10

Practical Voltage Source

Answer 10

A more accurate model of real voltage sources.

Represents the internal resistance of the source by placing a small resistance in series with an Ideal Voltage Source

Question 11

Source Transformation:

Basic Idea

Answer 11

Practical Current Sources can be electrically equivalent to Practical Voltage Sources.

Question 12

Source Transformation:

Equivalency Equations

Answer 12

A Practical Voltage Source has a Voltage V_s, and an internal resistance R_s in series with it.

The equivalent Practical Current Source has a current i_s and an internal resistance R_p in parallel with it.

For these to be equivalent:

R_s = R_p

v_s = R_pi_s = R_si_s

i_s = v_s/R_s

Question 13

Source Transformation:

Important Points

(8)

Answer 13

• Common goal:
  
  • End up with all current sources or all voltage sources
• Can be used repeatedly to simplify a circuit
• Resistor value stays the same, but is NOT the same resistor. Currents and Voltages associated with the resistor are lost
• If the resistor’s voltage or current controls a dependent source, it should NOT be used in source transformation
• If the resistor’s voltage or current is of interest, it shouldn’t be used in source transformation
• The head of the current source corresponds to the positive terminal of the voltage source
• To transform a voltage source: needs resistor in series
• To transform a current source: needs a resistor in parallel

Question 14

Source Transformation:

Transforming a Voltage Source

to a Current Source

Answer 14

For a resistor, R, in series with the voltage source, v_s,

Replace the voltage source with current source, i_s,

where i_s = v_s / R

and place the resistor in parallel with it.

Question 15

Source Transformation:

Transform a Current Source

to a Voltage Source

Answer 15

For a Current Source, i_s, in parallel with a resistor, R,

replace both with a Voltage Source, v_s,

where v_s = i_sR

Place the resistor in series with the voltage source.

Question 16

Thévenin’s Theorem:

Basic Idea

Answer 16

An arbitrarily complex linear circuit, with two terminals connected to some load,

can be fully represented by a Voltage Source and a Resistor in series.

Called a Thevenin Equivalent Circuit.

• V_th - is the open circuit voltage at the two terminals, and the value of the Voltage Source in the Equivalent Circuit
• R_th - the resistance at the terminals when independent sources are turned off. Also the resistance in the equivalent circuit

Question 17

Thévenin’s Theorem:

Steps to finding the

Thévenin Equivalent Circuit

Answer 17

1. Rearrange the circuit into two networks, A(circuit to be simplified) and B(the load), connected by 2 wires
2. Disconnect Network B. The voltage across the open-circuited two terminals is v_oc
3. Turn off every independent source in network A. Leave dependent sources.
4. Connect an independent voltage source with value v_oc in series with network A
5. Simplify to the equivalent resistance R_th​
6. Connect network B back to network A, B is unchanged

Question 18

Thévenin’s Theorem:

Turning off current sources

Turning off voltage sources

Answer 18

Turn off Current Source:

Replace with Open Circuit

Turn off Voltage Source:

Replace with Short Circuit

Question 19

Thévenin’s Theorem:

Two cases when finding R_th

Answer 19

No Dependent Sources:

R_th can be found by just turning off sources

Dependent Sources:

Turn off all independent sources, apply an arbitrary source at the terminals

Question 20

Norton’s Theorem:

Big Idea

Answer 20

A linear two terminal circuit may be replaced with an equivalent circuit containing a resistor, R_N and a current source, I_N, in parallel

It is similar to Thevenin’s Theorem, and the equivalent resistance is the same.

Question 21

Norton’s Theorem:

Relationship to Thévenin’s Theorem

Answer 21

The Norton equivalent Current, I_N is the ratio of the Thevenin Voltage, V_th and Resistance, R_th

I_N = V_th / R_th

If any two variables can be found, both the Thevenin and Norton equivalent circuits can be found.

Question 22

Norton’s Theorem:

Steps to finding the Equivalent Circuit

Answer 22

V_oc = R_th i_sc

1. Rearrange linear circuit into networks A and B, connected by two wires
2. Disconnect network B, short terminals of A. Define a current i_sc as the current through the short
3. Turn off independent sources in network A, leave dependent sources alone
4. Connect an independent current source with value i_sc in parallel with the inactive network
5. Connect network B back to network A

Question 23

Maximum Power Transfer Theorem

Answer 23

An independent voltage source in series with resistance R_s,

or an independent current source in parallel with resistance R_s,

or a network with Thevenin equivalent resistance R_s,

Delivers the maximum power to a load resistance, R_L, when the Load resistance matches the the source resistance

R_L = R_s

Question 24

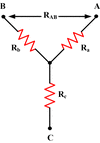
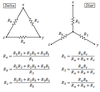
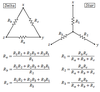
Delta Network:

Circuit Diagram

Answer 24

Question 25

Wye(Y) Network: Circuit Diagram

Answer 25

Question 26

Wye-Delta Conversion: Equations

Answer 26

Question 27

Delta-Wye Conversion: Equations

Answer 27