Ch 2 - Signal Detection and Absolute Judgement

Question 1

Signal detection theory

Answer 1

hits, misses, false alarm, and correct rejection

Question 2

Beta

Answer 2

ratio of neural activity produced by signal and noise at XC – intersection of noise and signal curves (critical threshold where operator decides “yes”)

Question 3

If signal and noise occur equally,

Answer 3

beta (β) = 1

Question 4

If signal and noise DO NOT occur equally

Answer 4

X_C should be moved left or right accordingly (β_OPT)

Question 5

Optimum beta βOPT

Answer 5

where beta SHOULD be set based on the probability of signal and noise

Question 6

Optimum beta

Answer 6

ratio of probability of no signal to probability of signal, expressed as value of correct rejection and hits to costs of false alarms and missies (13)

Question 7

Optimum beta

Answer 7

• Increase in numerator – high beta (value of correct rejection and cost of false alarms)

Question 8

Optimum beta

Answer 8

• Increase in denominator – low beta (value of hits and cost of misses) should lead to more liberal responding

Question 9

Sensitivity

Answer 9

• can help determine if misses come from high beta (conservativeness) or low beta (liberal responding)
• Higher d’, the more sensitive the receiver is

Question 10

ROC Curve

Answer 10

• receiver operating characteristics – joint influence of sensitivity and response bias
  
  • Uses P(H) and P(FA) as axis, as P(M) and P(CR) can be inferred by 1-P(H) and 1-P(CR)

Question 11

Fuzzy Signal detection theory

Answer 11

• in previous example, it is clear what is signal and what is noise, but this is not always possible in practice; sometimes the determination is fuzzy
  
  • Event in fuzzy SDT can belong to set signal (S) with some degree between 0 and 1
  • Or can belong to set response (r) between 0 and 1
  • Result of number of hits, misses, FAs, and CRs can then be computed
  • Example on page 19-20
    
    • Fuzzy hit rate = sum of all event H values/sum of membership values of signal S
    • FA rate = sum of FA values/sum of membership values of noise (1-s)
    • Once hit and FA rates computed, measures of sensitivity and bias can be calculated just as in conventional SDT

Question 12

• Applications of signal detection theory

Answer 12

• Medical diagnosis – making yes/no decision of whether an abnormality is present based on factors such as salience of abnormality, number of converging symptoms, and training of doctor
• Alarm and alarm systems – most have low beta threshold because the cost of misses is greater than the cost of false alarms
• Recognition/memory & eye witness testimony (22)

Question 13

• Vigilance paradigm – common application of SDT (25)

Answer 13

• Experiments have showed that vigilance lever is lower than desirable and declines steeply during first half hour of watch
• Measuring vigilance performance – based on factors that influence (increase of decrease) sensitivity and bias – listed on 26
• Arousal theory vs. sustained demand theory vs. expectancy theory (miss one signal and there is a perceived larger gap between signals, more likely to miss more)
• Techniques to combat loss of vigilance (28)

Question 14

• Absolute judgement (33)

Answer 14

• H_S = amount of info in the stimulus – base 2 log [e.g. - log₂] of the number of possible events
  
  • Example log₂ (4) = 2, log₂ (16) = 4
• H_{T =} amount transmitted to the response, which is between 0 and H_S
  
  • H_S – H_{T =} info loss (H_LOSS)

Question 15

• Information theory – (41)

Answer 15

• Number of alternatives, N
• H_S = log₂(N)
• Probability: H_S = log₂(1/P_i)
• Average information conveyed by a series of events with differing probabilities that occur over time – like a series of warning lights on a panel or a series of communication commands
  
  • H_AVE = – example page 43
  • HT Calculation example page 44

Question 16

• Stimulus Response Matrix (45) Figure 2S.2

Answer 16

Question 17

% redundancy

Answer 17

Question 18

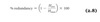
bandwidth

Answer 18

How rapidly info is transmitted