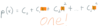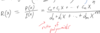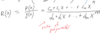Calculus (Columbia) Flashcards
Envision
how a
function is like a
machine.
A
_____ f is a
rule that assigns a
unique value
y = f(x) to each
input x ∈ D?
function
A
function f is a
_____ that assigns a
unique value
y = f(x) to each
input x ∈ D?
rule
A
function f is a
rule that assigns a
_____
y = f(x) to each
input x ∈ D?
unique value
A
function f is a
rule that assigns a
unique value
y = f(x) to each
_____ x ∈ D?
input
The
- *_____** of function f is the
- *set** of all
- *x ∈ ℝ**
s. t. - *f(x) is defined**.
domain
Picture:
A porn set where a domain-atrix with a red x over her nethers whipping an unsure British Red Guard gimp (who says “∈ℝ…”) while she screams “F(X) IS DEFINED!”
The
- *domain** of function f is the
- *_____** of all
- *x ∈ ℝ**
s. t. - *f(x) is defined**.
set
Picture:
A porn set where a domain-atrix with a red x over her nethers whipping an unsure British Red Guard gimp (who says “∈ℝ…”) while she screams “F(X) IS DEFINED!”
The
- *domain** of function f is the
- *set** of all
- *_____**
s. t. - *f(x) is defined**.
x ∈ ℝ
Picture:
A porn set where a domain-atrix with a red x over her nethers whipping an unsure British Red Guard gimp (who says “∈ℝ…”) while she screams “F(X) IS DEFINED!”
The
- *domain** of function f is the
- *set** of all
- *x ∈ ℝ**
s. t. - *_____**.
f(x) is defined
Picture:
A porn set where a domain-atrix with a red x over her nethers whipping an unsure British Red Guard gimp (who says “∈ℝ…”) while she screams “F(X) IS DEFINED!”
In set notation, the
domain of function f is
D = {_____ | f(x) is defined}.
x ∈ ℝ
In set notation, the
domain of function f is
D = {x ∈ ℝ | _____}.
f(x) is defined
The
domain of
f(x) = x2 is
_____.
D = ℝ
The
domain of
any polynomial is
_____.
D = ℝ
In set notation,
the
domain of
1
x − 1
is _____.
D = {x ∈ ℝ | x ≠ 1}
In inverval notation,
the
domain of
1
x − 1
is _____.
D = (−∞, 1) ∪ (1, ∞)
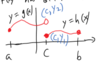
(a, b)
is an
[open / closed / neither]
interval (or set).
()pen
[a, b]
is an
[open / closed / neither]
interval (or set).
[ losed
[a, b)
is an
[open / closed / neither]
interval (or set).
neither
What is
[a, b]
in
interval notation?
[a, b] = {x ∈ ℝ | a < x < b}
What is
(a, b)
in
interval notation?
(a, b) = {x ∈ ℝ | a < x < b}
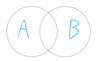
Envision
A ∩ B.
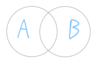
Envision
A ∪ B.
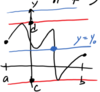
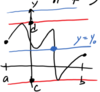
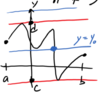
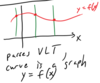
The
_____ of function f is the
set of all
possible values of y = f(x)
for some
x ∈ D.
range
The
range of function f is the
_____ of all
possible values of y = f(x)
for some
x ∈ D.
set
The
range of function f is the
set of
_____ of y = f(x)
for some
x ∈ D.
all possible values
The
range of function f is the
set of all
possible values of y = f(x)
for some
_____.
x ∈ D
In set notation, the
range of function f is
R = {_____ | y = f(x) for some x ∈ D}.
y ∈ ℝ
In set notation, the
range of function f is
R = {y ∈ ℝ | _____ for some x ∈ D}.
y = f(x)
In set notation, the
range of function f is
R = {y ∈ ℝ | y = f(x) for some _____}.
x ∈ D
The
domain of a function is the
[input / output] of that function
and represents the set of
all possible
[independent / dependent] variables
for that function.
input
independent
- INput*
- INdependent*
The
range of a function is the
[input / output] of that function
and represents the set of
all possible
[independent / dependent] variables
for that function.
output
dependent
“If you’re PUT OUT in the cold, you’re DEPENDENT on the kindness of others.”
In interval notation,
what is the
domain of this function?
D = [a, b]Next
In interval notation,
what is the
range of this function?
R = [c, d]
Analytically,
what is
Step 1 to determining whether a value is in the
range of a function?
Substitute
the value for the dependent variable
(i.e. y = f(x))
Analytically,
what is
Step 2 to determining whether a value is in the
range of a function?
Solve
for the independent variable.
(i.e. x)
After you’ve done all the work,
how do you know whether a value is in the
range of a function?
If you can
solve for the independent variable,
then the value is
in the range.
Given
f(x) = 1
x
is
- *0** in the
- *range** of f(x)?
No,
because you can’t substitute 0 for f(x) and then solve.
There is no such x-value.
Graphically,
how can you determine whether a graph is a
function?
The
vertical line test.
(not rigorous)
How do you know whether a
- *graph**
- *passes** the vertical line test?
If you
can’t draw a vertical line that
passes through more than one point
on the graph, then it
passes and is a
function.
This
fails the vertical line test, so it’s
not a function.
What do we have here?
An
implicit relation
between x and y.
(both are independent variables)
A
- *_____** function has
- *different functional forms** over
- *different domains**.
piecewise
A
- *piecewise** function has
- *_____** over
- *different domains**.
different functional forms
A
- *piecewise** function has
- *different functional forms** over
- *_____**.
different domains
How might this
function be defined?
Analytically,
polynomials are expressed as
p(x) = c0 + c1x + c2x2 + … + cjxn,
- *cj ___** and
- *n > 0 is an integer**
cj ∈ ℝ
Analytically,
polynomials are expressed as
p(x) = c0 + c1x + c1x2 + … + cjxn,
- *cj ∈ ℝ** and
- *_____**
n > 0 is an integer
(n ∈ ℤ, n > 0)
How many
variables can be in a polynomial?
One
In a
polynomial, the
coefficients can be
_____.
any real number
In a
polynomial, the
exponents of the variables can be
_____.
any nonnegative integer
A
- *_____** is a
- *ratio** of
- *polynomials**.
rational function
A
- *rational function** is a
- *_____** of
- *polynomials**.
ratio
A
- *rational function** is a
- *ratio** of
- *_____**.
polynomials
Analytically,
in an
odd function,
f(−x) = _____
−f(x)
Graphically,
an
odd function will
reflect about _____.
the y- and x-axes
or the
origin
O<span>dd</span>
O<span>rigin</span>
Analytically,
in an
even function,
f(−x) = _____
f(x)
Graphically,
an
even function will
reflect about _____.
the y-axis
Another way to
describe an
odd function is
_____.
odd symmetric
Another way to
describe an
even function is
_____.
even symmetric
Any
- *_____** with
- *all even powers** is
- *even symmetric**.
polynomial
Any
- *polynomial** with
- *all odd powers** is
- *_____**.
odd symmetric
Any
- *polynomial** with
- *_____** is
- *odd symmetric**.
all odd powers
Analytically,
f(x) is
non-decreasing over interval I = (a, b), if, for all
a < x1 < x2 < b,
_____.
f(x2) > f(x1)
Analytically,
f(x) is
non-decreasing over interval I = (a, b), if, for all
a < x1 < x2 < b,
_____.
f(x2) > f(x1)
Analytically,
f(x) is
_____ over interval I = (a, b), if, for all
a < x1 < x2 < b,
f(x2) > f(x1).
non-decreasing
Analytically,
f(x) is
_____ over interval I = (a, b), if, for all
a < x1 < x2 < b,
f(x2) < f(x1).
non-increasing
Analytically,
f(x) is
_____ over interval I = (a, b), if, for all
a < x1 < x2 < b,
f(x2) > f(x1).
increasing
Analytically,
f(x) is
increasing over interval I = (a, b), if, for all
_____,
f(x2) > f(x1).
a < x1 < x2 < b
Analytically,
f(x) is
increasing over interval I = (a, b), if, for all
a < x1 < x2 < b,
_____.
f(x2) > f(x1)
Analytically,
f(x) is
_____ over interval I = (a, b), if, for all
a < x1 < x2 < b,
f(x2) < f(x1).
decreasing
Analytically,
f(x) is
decreasing over interval I = (a, b), if, for all
a < x1 < x2 < b,
_____.
f(x2) < f(x1)
Over
x ∈ [0, 1], this function is
[increasing / decreasing / neither increasing nor decreasing].
increasing
Over
x ∈ [1, 2], this function is
[increasing / decreasing / neither increasing nor decreasing].
decreasing
Over
x ∈ [0, 2], this function is
[increasing / decreasing / neither increasing nor decreasing].
neither increasing nor decreasing
Pitfall:
When describing whether a
function is
increasing or decreasing, the
pitfall is
_____.
the interval
y = mx + b
is a
_____ function.
linear
y − y0 = m(x − x0)
is a
_____ function.
linear
f(x) = _____
is a
power function.
{ xp | p ∈ ℝ }
f(x) = { xp | p ∈ ℝ }
is a
_____ function.
power
Which are
power functions?
f(x) = **x<sup>−1/2</sup>** g(x) = **x<sup>π</sup>** h(x) = **x<sup>√(−1/2)</sup>**
Yes
Yes
No
The exponent
must be a real number,
although it can be
rational or irrational.
The
domain of a
power function is
_____.
D = ℝ
The
domain of
rational function
R(x) = n(x)
d(x)
is _____.
D = { x ∈ ℝ | d(x) ≠ 0}
Plainly,
how do you determine the
domain of a
rational function?
Set the denominator equal to zero.
The domain is everything but that.
What is this
asking about?
Analytically,
a function f(x) has a
_____ at level y = L if
limx→∞ = L
or
limx→−∞ = L
horizontal asymptote
Analytically,
a function f(x) has a
horizontal asymptote
at level y = L if
_____
or
_____.
limx→∞ = L
or
limx→−∞ = L
Plainly,
what is
Step 1 to finding a
horizontal asymptote?
Look to
- *highest-degree term** in
- *numerator and denominator**
Plainly,
what is
Step 2 to finding a
horizontal asymptote?
See if the highest-degree terms in
numerator and denominator
approach a finite number.
“When you’re taking a limit and the numerator and denominator are of the same degree, you’re typically going to get a finite number.”
