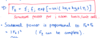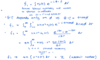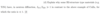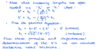Bramwell Flashcards
What is “Condensed Matter”?
Matter in a high-density state (i.e. solid, liquid, glass, colloid etc.) such that many-body (10^23) effects are important.
What is “order”?
Typically characterised by restricted phase space, low entropy and discrete symmetries; crystalline state is the paradigm.
What are “excitations”?
Excited quantum states reflect many-body nature: quasiparticle excitations in crystals are the paradigm.
Why X-ray and neutron scattering ?
Our understanding of condensed matter is intimately bound up with these experimental techniques, which are among the most important in science.
Why order and excitations in magnetism ?
Magnetic order and excitations are very diverse and illustrate all the general principles extremely well.
X-rays are
EM radiation, wavelength ~1 Angstrom
‘Thermal’ neutrons are
free quantum particles with wavelength ~1 Angstrom
X-ray photon, p k E
p = hbar*k, k = 2*pi/lambda, E = hbar*k*c
Thermal neutron, p k E
p = hbar*k, k = 2*pi/lambda, E = hbar^2*k^2/2m
Reciprocal Lattice Vector G of a cubic lattice
G = 2pi/a (h k l)
Reciprocal Lattice Vector G
By definition, G is a wavevector with the periodicity of the crystal, so
G=2pi/d_hkl
Direct Space and Reciprocal Space
orthorhombic structure
a=/=b=/=c, alpha=beta=gamma=90deg orthogonal
Basis vectors of reciprocal lattice
Sketch the basic experimental geometry of X-ray or neutron scattering in the ‘W’ (or ‘M’)- configuration. Appropriately annotate the different parts of your sketch
sample angle determines q (Wavevector)
analyser angle determines energy transfer deltaE = h*w_q
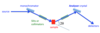
Scattering triangle for X-ray or neutron scattering.
Scattering vector def Q = k’ - k
Laue Condition
For a and Q to be parallel
Q.a=2pi*h
Where Q is the scattering vector
Show that the the scattering triangle is isoscelese for elastic scattering. Hence show that |Q| = 4pi sin theta/lambda. Write down the Laue condition for a and Q parallel and use the result just derived to demonstrate its equivalence to Bragg’s law.
First order (n = 1) Bragg reflection from an analyser crystal is used to measure the energy of a scattered X-ray or neutron.
Express how the energy of (i) the scattered photon and (ii) the scattered neutron depends on the scattering angle theta’ at the analyser crystal (d-spacing d_a).
Explain why the neutrons produced by a reactor or spallation source are typically passed through a hydrogenous material and what the process is called.
Neutrons produced by a reactor or spallation source are very high in energy and so have wavelengths too short to be useful in probing condensed matter. Passing them through a hydrogenous material slows the neutrons through collisions (hydrogen has a large scattering cross section) and the neutrons eventually equilibrate with the material, with a much lower energy. The process is called moderation and the material is called the moderator.
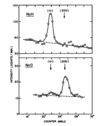
Argue that the Bragg peak becomes extremely intense and sharp in a real crystal
In real crystals, many atmoic planes are interfereing. This gives very sharp peaks surrounded by mostly destructive interference.
Scattering Amplitude A
Fourier Analysis
Fourier Analysis of electron density
Brillouin Zone
Wigner-Seitz unit cell of the reciprocal lattice
Weigner-Seitz Cell
The Wigner–Seitz cell in the reciprocal space is known as the first Brillouin zone.
It is made by drawing planes normal to the segments joining nearest lattice points to a particular lattice point, through the midpoints of such segments.
Partial Differential Cross-section Def
Differential Cross-section
Total cross-section def
Scattering Length def
X-ray electronic charge scattering
Neutron nuclear scattering
Neutron magnetic scattering
X-ray Diffraction Structure Factor, FG
in terms of electron density
L2 p.30
X-ray Diffraction Structure Factor for j atom basis/unit cell
j atoms in unit cell
fj form factor, gives an ‘envelope’ to the scattering pattern that reduces intensity of Bragg peaks at higher scattering angle
rest is phase factor, determines intensities in absence of form factor
X-ray Form Factor fj
X-ray form factor calculation
Ewald Construction
Neutron Nuclear Structure Factor FG
Magnetic Unit Cells
reflects the spin symmetry
Neutron Magnetic Structure Factor FG_M
form factor and spin-dependent factor (perp to scattering vector), and phase factor
Magnetic Structure Factor example
NOTE choice of cell.
Neutron Nuclear scattering question
PS2
Neutron Scat Question
Neutron Scat Q cont
The figure below shows classic powder neutron scattering data by Shull and Wollan. Comment on whether these patterns conform to the expectations discussed above.
As expected, the two patterns show the same peaks in the same positions but with very different intensities; the background is also much bigger in the case of NaH as expected
Q. Is Neutron or X-ray scattering preferable for determining structure in the following:
i) diamond
ii) KCl
i) x-ray: higher resolution due to higher intensity of x-rays. No reason not to use x-rays.
ii) Neutrons: to get contrast. K+, Cl- isoelectric. To x-rays these ions would appear almost the same, relying on subtle differences in the form factor (which to first approx is the same).
Q. Is Neutron or X-ray scattering preferable for determining structure in the following:
iii) CdCl2
iv) ice
iii) x-rays: Cd is highly absorbing of neutrons
iv) neutrons: H has practically no electrons, x-ray scattering is off electrons. (Though modern x-rays synchotrons could still resolve H). BUT using neutrons still has the problem of incoherent scattering (high background), but could deuterate.
What do the terms in this eq. represents, and where do they come from physically?
J - exchange constant, comes from overalp of the wavefunctions (think pauli principle)
D/E single ion anisotropy, comes from combination of crystal field effects with spin-orbit coupling
Crystallography Methods (3)
1) Rotating (single) Crystal method: Diffracted beam is counted in the detector by rotating the crystal through the Bragg condition. (collecting over an angular range)
2) Laue method (single crystal): Uses white beam (broad spectrum of wavelengths). Different λs pick out different lattice planes G = (hkl) -> patterns of diffraction spots on detector
3) Powder Method: A powder of a crystalline solid is a mechanical mixture of crystallines at many different orientation. -> Diffraction occurs in Debye-Scherrer rings, so diffraction information is reduced to being one dimensional.
Time of flight techniques (neutrons) used for powder diff in pulsed neutron sources, Rietvield method for modelling powder patterns (fit func to scattering rather than integrate bragg peaks)
‘define’ a crystal
A crystal is a state of matter with partial or discrete translational and rotational symmetry (when time-averaged and considered infinitely large). They have LOWER symmetry than time-averages liquids or gases, which has continuous symmetry.
X-ray absorption
Neutron absorption
Nuclear incoherent background
Advantages and disadvantages of neutron and x-ray scattering
coherent and incoherent scattering cross sections
Incoherent nuclear scattering - two types
i) isotopic incoherent
ii) nuclear spin incoherent
Incoherent nuclear scattering
bbar and b2bar
Incoherent nuclear scattering
scattering length b+/-
scattering functions S
correlation functions G
magnetomechanical parallelism
spin waves and magnons
magnon dispersion measured by inelastic neutron scattering
lots of magnetism stuff idc about
1D approx to FM, magnon dispersion is
hbar*w = 4JS(1-cosqa)
no. of modes with wavevector less than q
N = (1/8) * (4/3 pi q3) / (pi/L)3
eighth of sphere * vol of sphere / vol occupied by each mode!
ferromagnetic order parameter
magnetisation M(T)/M(0)
Bloch Law
M(T) = M(0) - CT3/2
