Basics Flashcards
Kerchoffs’ principle on Cryptography’s strength
If keys are:
- Kept secret
- Managed only by trusted systems
- Adequate length
Then it has no importance that the encryption and decryption algos are keps secret.
It is better that those algos are public so that they can be widely studied and weaknesses are identified and fixed.
Secret key / symmetric cryptography
- single key, shared only by the two parties.
- low computational loas > used for data encryption.
- Problem: how do we securely share the key among interested parties?
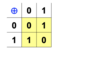
EX-OR function
The ideal confusion operator.
If the input is random the output will be equally random.
DES
- Data Encryption Standard
- Standard Federal Information Processing Standard 46/2 (FIPS)
- Key size: 56 bits + 8 parity bits.
- Datablock size: 64bits.
- Designed to be hardware efficient:
- requires only XOR/SHIFT/Permutation.
Triple DES (3DES, TDES)
- Repeated application of DES.
- Uses 2 of 3 56bits keys.
- MODES:
- DES - EEE3: 3-DES -> 3 different keys
- DES - EDE3: -> 3 different keys: E(k1, D(k2, E(k3, msg) ) ) [used for when compatibility with DES is wanted, in that case all keys are the same].
- DES - EEE2: Similar to DES-EEE3 but the first and third keys are the same
- DES - EDE2: Similar to DES-EDE3 but the first and third keys are the same
- Stanard FIPS 46/3 and ANSI X9.52 (X9 is prefix for banking and finance standards)
Double DES
- Double application of encryption algorithms is subject to known-plaintext attack named meet-in-the-middle.
- allows to decrypt data by attempting 2N+1 combinations (N = key size in bits)
- this is why double usage of encryption algos isn’t used often.
- computation time doubles, but the effective key-length is just another bit.
- Note that if the base symmetric algorithm would be a group, then it would exist K3 so that E(K2, E(K1, msg) = E(K3, msg).
- DES is not a group, otherwise 3DES = DES.
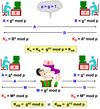
Meet-in-the-Middle attack
- Hypothesis
- N bit keys
- known P and C such that C = E(k2, E(k1, P) )
- Note:
- ∃ M such that M = E(K1, P) and C = E(K2, M)
- Actions:
- Compute 2N values Xi = E(Ki, P)
- Compute 2N values Yj = D(Kj, C)
- Look for Kj and Ki such that Yj = Xi.
- False positive can be discarded easily.
IDEA
- International Data Encryption Algorithm
- Patented with low royalty (commercial use)
- 128 bits key
- 64 bits data block
- Famous because it is used in PGP
- Operations:
- XOR
- ADDITION mod 16
- MULTIPLICATION mod 216 + 1
RC{2,4}
- Ron Rivest invention
- RC = RON’S CODE
- Proprietary algorithm (owned by RSA) but not patented
- 3-10x faster than DES
- RC2 is a block algo
- RC4 is a stream algo
- Key length is not fixed
RC2 was published as RFC-2268 in 1998, 8 to 1024 bits keys (usually 64bits), 64b datablock.
RC4 reverse engineered (ARCFOUR).
Application of block algorithms to data blocks of size != algorithm’s block size.
- To encrypt data size > algo’s block size
- ECB (Electronic Cod Book)
- CBC (Cipher Block Chaining)
- To encrypt data size < algo’s block size
- Padding
- CFB (Cipher FeedBack), OFB (Output FeedBack)
- CTR (Counter mode)
ECB
Electronic Code Book
- Encryption:
- Formula: Ci = enc(K, Pi)
- Can’t be used on messages > algo block size because swapping of blocks goes undetected.
- Identical blocks generate identical cyphertext, thus it is vulnerable to known-plaintext attack
- Decryption:
- Formula = Pi = dec(K, Ci)
- A trasmission error generates an error at decription of the block.
CBC
Cipher Block Chaining
- Encryption
- Formula: Ci = enc(K, Pi xor Ci-1)
- Requires C0 = IV (Init. Vector)
- IV changes at every message, so that pre-computation cannot be performed
- IV is sent in clear to the receiver
- IV should be a nonce (number used once)
- Decryption:
- Formula: Pi = dec(K, Ci) xor Ci-1
- An error in trasmission generates and error at the decryption of two blocks.
Padding
- B = size of algo block
- D = size of data to process
- Used for aligning and filling
- Padding: add bits until a multiple of the algo block size is reached.
- Problems:
- We store/transmit more data than needed.
- What value do we use to do padding?
- Padding Techniques:
- If message length is known: add null bytes
- Original DES: one 1 bit followed by many zeros
- one byte with value 128 followed by null bytes: 0x80 0x00 0x00
- last byte’s value equal to the length of padding: 0x?? 0x?? 0x03
- Padding with exlicit length L:
- (Schneier) NULL bytes eg.: 0x00 0x00 0x03
- (SSL/TLS0 bytes with value L, e.g.: 0x03 0x03 0x03
- (SSH2) random bytes, e.g.: 0x05 0xF2 0x03
- (IPSec/ESP) progressive number, e.g.: 0x01, 0x02, x03
- byte with value L-1, e.g.: 0x02 0x02 0x02
Notes:
- Some offer minimal integrity control:
- if key is wrong or data is manipulated, the padding bytes are incoherent (e.g. Padding length > Block size, or wrong padding values)
- Don’t design your own padding, read books instead.
- Typically applied to large data, on last fragment.
- if |D| < |B| we prefer ad-hoc techniques (CFB, OFB, CTR, …)
- padding is always added to avoid interpretation errors, even if |D| is a multiple of |B|
- The type of padding used in algorithms determines some of the possible attacks
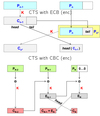
CTS
Ciphertext Stealing
- CTS permits to use block algorithms without padding
- last (partial) block filled with bytes from the second-to-last-block
- these bytes are removed from the second-to-last block (which becomes a partial one)
- after encryption, exchange the position of the last and second to last blocks
- useful when we cannot increase the size of the data after encryption: when the HDD is full you can’t use padding.
- the computation time slightly increases
In CBC the tail of the second-to-last block got xored with the padding of the last block, so we have it.
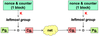
CTR
Counter mode
- Uses a block algorithm to encrypt N bits at a time (a “group”, often a byte)
- random direct access to any ciphertext group
- requires a nonce and a counter (concatenated, summed, XORed, …)
- trasmission error results in having an error only in one group
- Enables encryption/decription of a specific block without performing it for the whole message.
*
Symmetric stream algorithms
- operate ona a stream of data without requiring the division on blocks, typically on one bit or byte at a time
- ideal algorithm:
- one-time pad (requires a key as long as the message to protect)
- real algorithms:
- use pseudo-random key generators, syncrhonized between sender and receiver
- if an attacker deletes a message sync. is lost -> communication is broken
- example: RC4, SEAL
- EU sponsored a competition for stream cipher in 2008, that resulted in the selection of an algorithm portfolio for software and hardware.
Salsa20, ChaCha20
Symmetric stream algorithms invented by DJ Bernstein
128 or 256 bit keys
- ChaCha20 is an improvement of Salsa20
- more diffusion of bits
- faster on some archs.
- base operation: 32bit ARX (add - rotate - xor)
- base function: f(key256, Nonce64, Counter64) = 513-bit keystream block
- permits O(1) decryption of any block at random
- Salsa20 performs 20 mixing rounds of the input
- Salsa 20/12 and Salsa20/8 make 12 and 8 mixing rounds (faster but less secure)
- ChaCha20 was standardized and adopted (IETF has slightly modified the original specification)
Symmetric encryption
- single and secret key
- one for each couple (or group!) of users
- Key distribution:
- for N parties, N(N-1)/2 keys are necessary.
- distribution can be Out Of Band or by meanch of key exchange algorithms.
- Length of secret keys:
- if the encryption algo was well designed and the keys are kept secret, then the only possible attack is brute force, that requires 2Nbit attempts.
Length of cryptographic keys in relation with security
DES challenges
- Total of 3
- 1st took 5 months to break (distributed computing)
- 2nd 1 month (distributed computing)
- 3rd 2 days: 1 special-purpouse sysem (deep crack) developed by EFF at the cost $250k
- there was an assumption about the encoding (ASCII)
- 4th: 22 hours
- DEEP CRACK + a few thousands workstations
- Doesn’t mean that DES is weak, just that the key is short.
- 3DES could not be decrypted by DEEP CRACK
IETF changed all RFC advising not to use DES, but 3DES.
AES
US competition called for selecting a new symmetric algorithm.
AES (Advanced Ecryption Standard)
- key length up to 256 bits.
- block size of at least 128 bits.
5 finalists, RIJNDAEL won in 2000, published in 2001 a FIPS-197 => AES = RIJNDAEL.
Gradually being adopted since 2010, encryption algos are like wine, the bests are the one that ages.
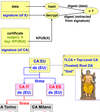
Public key criptography
- k1 != k2
- asymmetric algorithms
- pair of keys (public and private): one used for decription and the other for encryption.
- high computational load
- used to distribute secret keys and create electronic signature (with hashing)
- main algos:
- Diffie-Hellman, RSA, DSA, El Gamal
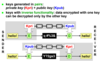
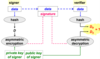
Digital Signature
- Digital signature asymmetric encryption of data made with the private key of the author
- Since asymmetric encryption is very slow, usually only a summary of the message is encrypted
- provides data authentication and integrity
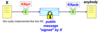
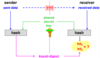
Confidentiality without a shared secret
- Given the public key of a receiver, it is possible to create a secret message that only the receiver can decrypt.
Public Key Algorithms
- RSA
- product of prime numbers, factoring of the result
- usable for secrecy and digital signatures
- patented (only in USA) by RSA, expired in 20-09-2000
- computational optimizations:
- all public keys have E = 3, 17 or 65537 (0x10001, fermat number)
- the power operation is very easy since these numbers have only two bits to 1
- high speed of encryption and signature verification
- optimized algorithms for this special calse
- Possible attack: provide signature made with key whose exponent has > 2 bits to one, since the algorithms are not efficient with those keys it willl generate a high computational load.
- DSA (Digital Signature Algorithm)
- taking the power, logarithm of the result
- digital signature only (uses one-way lossy compression)
- for encryption it uses the El-Gamal algorithm
Length of public keys and relative time in which they can be attacked (atm)
- 512 bits can be attacked in some weeks
- 1024 bits can be attacked in some months
- 2048 bits offer an appropriate security level for several years
- Note that MS system don’t accept any RSA keys < 1024 since 2012; Mozilla does not accept keys < 2048 & md5 since 2013
Secret key exchange by asymmetric algorithms
- confidentiality without shared secrets is often used to send the secret key chosen for a symmetric algorithm
*
Diffie-Hellman
- First public key algorithm invented
- Frequently used to agree on secret key.
- Resistant to the sniffing attack
- If the attacker can manipulte the data then it is possible to make a man in the middle attack: to protect from MITM we need pre-authentication (certificates for DH keys, authenticated DH = MQV)
How
- A and B agree to use two public integers p (prime, large) and g (generators) such that: 1 < g < p ( typically g=2,3,5 )
- DH key length = bits of p
- A arbitrarily chooses an integer x > 0 and computes: X = gx mod p
- B arbitrarily chooses and integer y > 0 and computes: Y = gy mod p
- A and b exchange (publish) X and y
- A computes KA = Yx
- B computes KB = Xy
- KA = KB = gxy mod p
Elliptic curve cryptography
- Instead of using arithmetic, the operations are executed on the surface of a 2D (elliptic) curve
- The problem of discrete logarithm becomes harder on these curves, hence it is possible to reduce the length of the keys to have comparable security.
- Digital signatures = ECDSA
- Key agreement = ECDH
- Authenticated key agreement = ECMQV (patented)
- Key distribution = ECIES (EC Integrated Encryption Scheme)
Hash functions
They usually split the message M in N blocks (M1, …. Mn) and iteratively apply a base function (f)
Vk = f(Vk-1, Mk) with V0 = IV and h = VN
SHA-3
- Competition started in 2008 with 64 candidates, the winner was declared in 2012: Keccak (“catch-ack”)
- SHA-3 family has many hash functions
Authentication by means of keyed-digest
A way to intrinsically secure the digest, since it cannot be exchanged out of band.
The digest is calculated on the message and on the secret key.
Operations:
- Sender: d = digest(K, M)
- Transmission: M || d
- Receiver: d’ = digest(K, M)
- Verification: is d == d’?
Only entities that know the key can compare the transmitted digest with the digest calculated on the received data.
Advantages:
- Only one operation needs to be performed (digest computation)
- few additional data
Cons:
- Does not provide non-repudiation.
Possible mistakes in computing keyed-digest:
- if kd = H(K || M) an attacker could add a message block to the end
- kd’ = H(K || M || M’) = f(kd, M’)
- if kd = H(M || K) an attacker could add a message to the beginning of the message
- kd = H(M’ || M || K), choosing M’ s.t. IV = f(IV, M’)
- to protect against these attacks:
- insert the length of the message in the digest
- define kd = H(K || M || K)
- use a standard key digest.
Authenticated encryption
Combine privacy and authentication (and integrity), has many benefits:
- Just one key and one algorithm
- high speed
- less error likelihood in combining 2 functions
- Useful for many applications (e-mail messages, network packets, …)
- Normal encrytion modes are vulnerabe to chosen ciphertext attacks when on-line: Attacker modified ciphetext and observes whether the receiver signaled an error (e.g. padding oracle or decryption oracle attack).
In the picture: AEAD (Authenticated Encryption with Associated Data), one way of making AE possible. Note that AEAD is spliting the message in: part that needs integrity and part that needs privacy . The nonce is added to avoid replay attacks. The encrypted payload also includes a tag that provides integrity for the header and the nonce.
IGE
(Infinite Garble Extension)
Basically, it is like the CBC with one addition: in CBC a modification in one block of the ciphertext affect only the block itself and the next one (and then propagation stops). IGE makes it so that an error will occur on every block after the tampered one.
In this way verifying the validity of the message requires only to decrypt the last block to check if it contains the expected value (some fixed content: all zeros, content length, etc.)
In this context the last block is what in AEAD is called tag.
Not a very good algo, but interesting.
Digital signature
Authentication by means of digest, using asymmetric crypto.
Keyed digest doesn’t provide non-repudiation.
- (signer S) H = enc( S_Kpri, hash( M ) )
- (transmission) M || H
- (verifiier V) X = dec( S_Kpub, H )
- (verification) if ( X == hash( M ) ) then OK else ALARM!
Problem: guerantee of association between identity and public key.
Attack: tampering the digital signature will result in an error, but it cannot be determined if it is because of a tramission error in the signature or in the message.
Public key certificate
A data structure used to securely bind a public key to some attributes.
Binds a key to an identity, but supports also other kinds of associations (ip addresses).
The binding is secured by a certificate authority that digitally signs the public key certificate, so that:
- we have a proof of authentication: it is a valid certificate because it has been created by a certification authority.
- a proof of integrity: the has not been modifyied.
- has a limited validity, like a identity document, and can also be revoked by the user or the issuer. It is responsability of the receiver to check that the certificate is still valid.
Verification:
- To verify a signature, we request the public key certificate that is signed by the entitiy that provides, then we need to verify the public key of the Certificate Authority, and in-turn of the Certificate Authority that hosts its public key certificate, continue like this until we react the Root CA, this cannot be verified, it is self-signed.
There are multiple TLCA. Tipically in a computer system there are lot of trusted CA: for security (so that no one entity can control who is trusted) and since obtaining a certificate by a CA has a price. (CA pay to be in the list of trusted CA of Windows for example).
Problem: attackers could fake the whole CA tree, if the device is left unattended and the attacker manages to have administrative privileges, it is possible to add another (fake) Root CA, making the whole hierarchical system useless for that device. The list of Root CA can be managed either by the operating system or by the application being used.
Structure of a X.509 certificate
- Version: since there are more versions of the same format as seen previously;
- Serial number: each certificate is uniquely identified;
- Signature algorithm: algorithm used to perform the signature;
-
Issuer: name of the entity that created the certificate, the certification authority. The syntax used to specify this information is called DN (distinguished name), composed by three fields:
- C stands for country (e.g. Italy);
- O stands for organization (e.g. Politecnico di Torino);
- OU stands for organizational unit, which means that this is the department who created this certificate (e.g. certification authority).
- Validity: period of validity.
-
Subject: the entity that is controlling the private key corresponding to the public key being certified. Also, here it is used the DM to identify that entity, with other fields not mentioned earlier:
- CN stands for common name (e.g. Antonio Lioy);
- Email, that is the e-mail of the entity. It is important to include this fields because public key certificates are used to protect internet applications, for example to send an e-mail to “Antonio Lioy”, the mail server needs to be able to understand what is the certified mail for the entity (so, the e-mail field is required). The same reasoning applies to other applications for which protection is wanted.
- subjectPublicKeyInfo: is the field containing the public key; it specifies the algorithm, the length of the key and all the bits that constitute it;
- CA digital signature: it is the digital signature of the certification authority computed over the certificate.
Crypto performance
Depends on CPU, not on ram.
Performance is not a problem on clients (if not embedded systems).
Perfmance is an issue on servers when making secure a network of ndoes (e.g. routers), in these cases special hardware is used, either for crypto functions or for the whole packet processing step (including crypto stuff).
- RC4 is the best of all cause it’s a stream algo.
- 3DES is 3x slower than DES.
- AES is faster than DES and guarantees better security.
- Singnature verification is faster than creation.
Step-up (gated) cryptography (dec’98)
User browser uses weak crypto generally, and strong crypto when it talks with a bank.
It is also named gated cryptography because the strong part is inside a gate opened only when the server submits the correct certificate.
