Basic Definitions and Results Flashcards
General Linear Group

Centre (of a group)
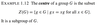
Quaternion Group
Multiplication determined by:
i2=-1=j2, ij=k=-ji
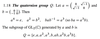
Cayley’s Theorem Corollary


Simple Facts about Cosets
(4 facts)

Lagrange’s Theorem

Normal Subgroup

Normal subgroups and cosets

Three examples of normal subgroups

Simple group

Products of Subgroups

Normal subgroups

Special linear group of degree n
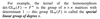
Universal property for quotients

Homomorphism Theorem


Isomorphism Theorem



Special case of Correspondence Theorem

Direct Product

Two propositions for determining if a group is the direct product of two subgroups


Proposition to determine if a group is the direct product of n subgroups

Example for corollary:


Theorem: Classification of groups

Summary: finite groups

Character of a group

Quadratic residue modulo p

Dual group (and theorem)

Orthogonality Relations (character of a group)

The order of ab

For any map of sets alpha:X –> G from X to a group G, there exists a unique homomorphism FX –> G making the following diagram commute:

Universal property of the inclusion X–>FX characterizes it

Let G be the group defined by the presentation (X,R). For any group H and map of sets alpha:X –> H sending each element of R to 1 (in the obvious sense), there exists a unique homomorphism G –> H making the following diagram commute



