AS Flashcards
What are the indices rules?
When should you complete the square?
When a quadratic equation will not factorise easily
How do you complete the square? (using x2 +yx + c)
Write in the form (x + y/2)2 -(y/2)2 + c
Complete the square of x2 + 6x + 7?
(x+3)2 -32 + 7
= (x+3)2 -2
Complete the square of 2x2 + 8x + 7?
2[x2 + 4x + 7/2]
= 2[(x+2)2 -22 + 7/2)
= 2[(x+2)2 - 1/2]
= 2(x+2)2 - 1
How woulkd you complete the square of -x2 + 4x + 5
= -1[x2 -4x -5]
Then complete as normal to get
-1(x-2)2 + 9
What is the quadratic formula?
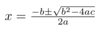
What is the discriminant of the quadratic formula?
b2 - 4ac
What happens when b2 - 4ac > 0 ?
There are two real distinct roots
What happens when b2 - 4ac = 0 ?
There is one real root (repeated)
What happens when b2 - 4ac < 0 ?
No real roots
What are the inequality symbols?
Same for not equal to but circle not shaded in
How can you tell the line of symetry from completing the square?
(x + y)2 + c
Curve is left by y and up by c
What is a transformation of y = f(x-a)?
Transformation of the graph by (x+a,y)
What is the transformation of y = f(a) + b?
Graph is transformed by (x,y+b)
What is the transformation of y = af(x)?
Graph is strechted by scale factor a (parallel to y-axis)
(x,ay)
What is the transformation of y = f(ax)?
Transformation of graph by 1/a parallel to x axis
((1/a) x, y)
What is the transformation of y = -f(x)
Reflection of graph in x-axis
(x, -y)
What is teh transformation of y = f(-x)?
Reflection of graph in y-axis
(-x, y)
What order should be done with 2f(x+1)?
Stretch then translate
What is the sine rule?
a/sinA = b/sinB = c/sinC
sinA/a = sinB/b = sinC/c
What is the cosine rule?
a2 = b2 + c2 -2bc x cosA
What is the area of a non-right angle triangle ?
Area = 1/2 x base x height
Area = 1/2 x a x b x sinC
What is the lowercase and uppercase letters in triangles?
Lowercase - side
Uppercase - Angle
What are some values for the graph y=sinx ?
x = 0, y = 0
x = 90, y = 1
x = 180, y = 0
x = 270, y = -1
x = 360, y = 0
What are some values of y=cosx?
x = 0, y = 1
x = 90, y = 0
x = 180, y = -1
x = 270, y = 0
x = 360, y = 1
What is tanx equal to?
tanx = sinx/cosx
What are some values of y=tanx?
x = 0, y = 0
x = 90, y = ∞
x = 180, y = 0
x = 270, y = ∞
x = 360, y = 0
How do you find the values of sine after getting the principle value?
PV & 180 - PV
Repeat every 360
How do you find the values of cosine after getting the principle value?
PV, 360 - PV
Every 360
How do you find the values of tan after getting the principle value?
PV, PV +/- multiples of 180
What is the equation that links sin2x and cos2x?
sin2x + cos2x = 1
What is the √ (xy) ?
√ x * √ y
What are the forms of equations of a straight line?
y -y1 = m(x-x1)
ax + by + c = 0
What are the gradients of two lines for them to be perpendicular?
m1 * m2 = -1
m1 and m2 are the gradients of each line
What are the gradients for two straight lines to be parallel?
m1 = m2
What is the equation of a circle?
(x-a)2 + (y-b)2 = r2
r - radius
a = x coordinate
b = y coordinate
What is the angle in a semicircle theorem?
Angle subtended across a circle’s diameter is always a right angle
What is the theorem involving angles at the centre and circumference of the circle?
The angle subtended at the centre is twice that at the circumference
What is the theorem relating angles in the same arc?
Angles subtended by the same arc are equal
What is the theorem relating cyclic quadrilateral?
Opposite angles in cyclic quadrilaterals add up to 180º
What is the angle between a tangent and the radius of a circle?
90º
What theorem relates chords and the centre of a circle?
Perpendicular from the centre of a circle bisects the chord
