Arbitrage Theory and Options

Question 1

Define Asset Span

Answer 1

The set of different payoffs we can achieve in the future via trade in the existing assets today. Typically denoted by M

Question 2

Define Complete markets

Answer 2

Market are complete if any newly issued security can be replicated by current assets. M = R^s

Question 3

Wat is the relation between M and R^s in incomplete markets?

Answer 3

M is a subset of R^s

Question 4

Define arbitrage

Answer 4

Making a certain profit with zero initial capital. hx >= 0 and ph’ <= where one holds with strict inequality

Question 5

Define a strong arbitrage

Answer 5

Zero or positive payment tomorrow. Positive payment today

Question 6

State the law of one price mathematically

Answer 6

Question 7

State the law of one price qualitatively

Answer 7

Any two portfolios with the same payoffs must have the same price

Question 8

Define a risk-premium

Answer 8

Question 9

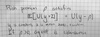
How toderive risk-neutral probabilities?

Answer 9

Define security price as a inear combination of the state prices. Divide and multiply by the sum of state prices. Each risk-neutral probability is the state-price divided by the sum of state prices

Question 10

What is the Covered interest rate parity?

Answer 10

F = S * (1+r*)/(1+r)

F and S are forwards and spot prices measured as amount of fx per domestic currency

r* is foreign interest rate. r i domestic currency

Question 11

How to derive the CIRP?

Answer 11

Borrow 1/(1+r) at home (need to repay 1)

Buy foreign FX

Invest abroad

Sell forward fx, 1/F

1/(1+r) * S * (1+r*) * (1/F)

Since you will have to repay only 1, the payoff to this strategy must be 1 for there not to be arbitrage

Question 12

What are portfolio holding in vector form?

Answer 12

h = (h1, h2, … , hj)

Question 13

What is portfolio payoff in vector-matrix notation?

Answer 13

hX

Question 14

What is the regular formulation of the Fundamental Theorem of Finance?

Answer 14

Theorem 1:

Security prices exclude arbitrage iff there exist strictly positive state prices

Theorem 2:

Security prices exclude strong arbitrage iff there exist positive state prices

Question 15

How does market completeness relate to ‘no arbitrage’?

Answer 15

No aribitrage requires existence, not uniqueness, of positive state prices. We can still price redundant assets in incomplete markets

Question 16

Define Absolute Risk Aversion?

Answer 16

A(w) = - u’‘(w) / u’(w)

Question 17

Define Relative Risk Aversion

Answer 17

RRA = - u’‘(w)/u’(w)*w = A(w) * w

Question 18

What is the “general” fundamental theorem of finance=

Answer 18

Equillibrium is a sufficient condition for ‘no arbitrage’ which is a necessary and sufficient condition for positive state prices

Question 19

What is dynamic completion and when is it possible?

Answer 19

It is completing the market by retrading. Allows for completing markets when number of assets is below number of states. Requires that the maximum number of states from each note does not exceed the number of securities

Question 20

What is the upper bound for the price of a call?

Answer 20

c <= S

Question 21

What is the lower bound for the price of a call?

Answer 21

c >= S - K/(1+r)

Question 22

What is put call parity?

Answer 22

c + k/(1+r) = p + S

Question 23

How can options complete the markets?

Answer 23

Imagine the market has one asset which pays a different payoff in each state. Then issue s-1 options with strike price at the assets payouts (except fore the largest)

Question 24

What is the welfare effect of completing the markets?

Answer 24

Fully completing the markets will always have a positive welfare effect.

Partially completing the markets need not make people better off. May generate externalities, requiring regulation

Question 25

What is the value difference between European and American options?

Answer 25

American options are worth at least as much as European options. An American call should never be issued early, so should have the same price. American puts may be exercised early with benefit

Question 26

Define delta hedgin

Answer 26

A hedging portfolio such that the payoff is the same in the up and down state. Portfolio holds option and stock in correct proportions. Holds delta of the stock and -1 option.

Question 27

How to find the risk-neutral probability?

Answer 27

q = (1 + rf - d) / (u - d)

if u and d are gross. If they are net, replace “1 + rf” with “rf”

Question 28

What is an asian option?

Answer 28

An options for which the strike price is set equal to the average value of the underlying over the life of the option?