Anti-derivatives & Integration Formulas (initial version)

Question 1

Answer 1

Question 2

Answer 2

Question 3

Answer 3

Question 4

Answer 4

Question 5

Answer 5

Question 6

Answer 6

Question 7

Answer 7

Question 8

Answer 8

Question 9

Answer 9

Question 10

Answer 10

Question 11

Answer 11

Question 12

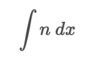
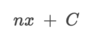
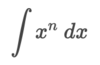
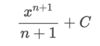
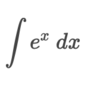
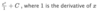
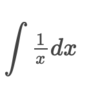
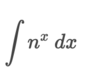
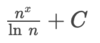
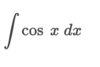
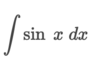
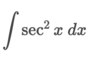
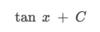
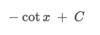
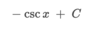
How can we integrate this problem?

Answer 12

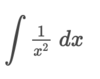
By using the power rule. ln x + C only works when the power of x is equal to 1 (x¹)

Question 13

Answer 13

Question 14

Answer 14

Question 15

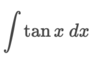
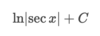
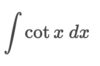
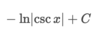
Write the general formula used in integration by parts

Answer 15

• Here, you want to find two things: u and dv
• After identifying those two elements, you need to find du by differentiating u and you need to find v by integrating dv

Question 16

Decode the acronym LIATE (for identifying the ‘u’ value)

Answer 16

Logs > Inverse trigs > Algebraic > Trigs > Exponential

• Logs: things like “ln” and “log”
• Inverse trigs: things like “cos^-1” or “tan^-1“…etc
• Algebraic: things like “x” or “x²” or “x³” or polynomials
• Trigs: things like “sin” or “tan” …etc
• Exponential: things like “e^x” and “a^x”

Question 17

What are the two main techniques used in solving integration by parts problems?

Answer 17

1- The LIATE rule (helps with identifying the ‘u’ term, then you should proceed with the original by parts formula)

2- The tabular method

Question 18

Answer 18

Question 19

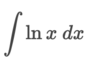
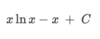
Can I use the tabular method for solving all integration by parts problems?

Answer 19

Yes!

You can use it for all IBP problems

Question 20

How to know if I chose the correct u and dv terms?

Answer 20

Choose your u and dv based on the LIATE rule (should work perfectly for most problems):

1- If your problem is getting simpler, then your choice was correct

2- If the problem is getting more complicated (especially at the ∫ v du part), then you probably have to go back and switch the values of those two (u and dv) and try again

Question 21

When to use the u-substitution technique?

Answer 21

When the anti-derivative and the derivative of a given function are available in the same problem

Question 22

When to use the integration by parts technique?

Question 23

How many possible scenarios we can expect while solving IBP problems with the tabular method?

Answer 23

3 different cases:

• case 1: when the n^th derivative of u is equal to zero (after taking the derivative of u for an x number of times). Example: ∫ x²cosx dx
• case 2: when the n^th derivative of u will never be zero, but the function of the integral repeats itself in the table. We have to stop as soon as we see the first match (regardless of the sign and/or any multiplied constants). Example: ∫ e^x sinx dx
• case 3: when the n^th derivative of u will never be zero, but the n^th derivative of u keeps getting smaller and smaller. In this case, we have to stop right after finding the first derivative of 2 and consider the first two rows of the table in our final answer. Example: ∫ x³ lnx dx

Question 24

What is the purpose of using the u-substitution technique?

Answer 24

The ultimate goal of using this technique is to cancel out all Xs in the problem and be left with Us only (hence the name)

Question 25

Trig integrals (section 8.3) depends on your knowledge in the following:

Answer 25

1- Knowing the required identities

2- Knowing the cases and what to do in each case (4 cases in total)

3- Applying u-substitution correctly right after using one of the Pythagorean identities (from #1)

4- Knowing the derivatives and anti-derivatives of all trigs

Question 26

How many different cases we have for trig integrals (section 8.3)?

Answer 26

Two different cases:

1- Integrals involving sin and cos

2- Integrals involving tan and sec

Question 27

What are the two cases or rules we have to know when we have sin and cos (section 8.3)?

Answer 27

CASE 1: When m (power of sin) AND/OR n (power of cos) is odd

• If the power of sin is odd, keep one factor of sin factored out and use the Pythagorean identity to change sin²x = 1 - cos²x
• We will do the same thing if the power of cos is odd, but we will be using cos²x = 1- sin²x instead
• If both of m and n are odd, then pick the one with the smaller power and factor out one factor of it and use the corresponding Pythagorean identity

CASE 2: When m and n are both even

• In this case, we have to use one of the half angle identites to solve the problem

Question 28

What are the two cases or rules we have to know when we have tan and sec (section 8.3)?

Answer 28

CASE 1: If the power of tan is odd

• In this case, keep one factor of (sec x tan x) factored out and use the Pythagorean identity of tan²x = sec²x - 1

CASE 2: If the power of sec is even

• In this case, keep one factor of sec²x factored out and use the Pythagorean identity of sec²x = tan²x + 1