Algorithms Flashcards
(34 cards)
What is an algorithm?
A process or set of steps to accomplish a certain task.
Why do I need to know algorithms?
It is the foundation for being a successful problem solver and developer.
What are the 5 steps to take to best solve a problem?
- Understand the problem
- Explore concrete examples
- Break it down
- Solve/Simplify
- Look back and refactor
When solving a problem, what are the 5 steps/questions that can help to better understand the problem?
- Can I restate the problem in my own words?
- What are the inputs that go into the problem?
- What are the outputs that should come from the solution of the problem?
- Can the outputs be determined from the inputs of the problem. or do I have enough information to solve the problem?
- How should I label the important pieces of data that are part of the problem?
When solving a problem, what are the 4 steps to take when exploring examples?
- Start with simple examples 2. Progress with more complex examples 3. Explore examples with empty inputs 4. Explore examples with invalid inputs
When solving a problem, how do you break down the problem? And why would you break it down?
By explicitly writing out the steps you need to take, in pseudocode or comments. It forces you to think about your approach and the code you are going to write before you write it, and helps you catch any lingering conceptual issues or misunderstandings before you dive in and have to worry about details (e.g. language syntax) as well.
When solving a problem and getting stuck, what are the 4 steps to take to simplify the problem?
- Find the core difficulty in what you are trying to do 2. Temporarily ignore that difficulty 3. Write a simplified solution 4. Then incorporate that difficulty back in
When solving a problem, what are the 5 ‘look back and refactor’ questions to ask yourself?
- Can I check the result? 2. Can I understand it at a glance? 3. Can I improve the performance of the solution? 4. Can I derive the result differently? 5. Can I think of other ways to refactor?
In JavaScript, how to use a regular expression to check if a character is an alphanumeric character?
/[a-zA-Z0-9]/.test(character)
Returns true if it finds a match, otherwise it returns false Note: Regular expressions do not have the best performance; checking ASCI character code value (using string.charCodeAt(index)) could be about 50% faster.
Name 7 of the most commonly used problem solving ideas or patterns.
- Frequency Counter
- Multiple Pointers
- Sliding Window
- Divide and Conquer
- Dynamic Programming
- Greedy Algorithms
- Backtracking
What is the idea behind Frequency Counters,, and how do they improve performance?
The Frequency Counters pattern uses an object or set to collect values/frequencies of values.
They often avoids the need for nested loops or O(n^2) operations with arrays/strings.
What is the idea behind the Multiple Pointers pattern, and how do they improve performance?
The Multiple Pointers pattern creates values (pointers) that correspond to an index or position, and move towards the beginning, end or middle based on a certain condition.
This pattern is very efficient for solving problems with minimal space complexity.
What is the idea behind the Sliding Window pattern, and what is it useful for?
The Sliding Window pattern involves creating a window which can eiter be an array or number from one position to another. Depending on a certain condition, the window either increases or closes (and a new window is created).
The Sliding Window pattern is useful for keeping track of a subset of data in an array/string etc.
What is the idea behind the Divide and Conquer pattern, and what is its biggest advantage?
The Divide and Conquer pattern involves dividing a data set into smaller chunks and then repeating a process with a subset of data.
The Divide and Conquer pattern can tremendously decrease time complexitiy.
What is a recursive function, and how does it affect the call stack?
A recursive function is a function that keeps calling itself until it reaches a base case. A recursive function keeps pushing new functions onto the call stack.
Explain the use of the call stack in regards to functions?
- Any time a function is invoked it is placed (pushed) on the top of the call stack.
- When the compiler sees the return keyword or when the function ends, the compiler will remove (pop) the function from (the top of) the stack.
What are three essential parts of a recursive function?
- Base case: the condition when the recursion ends. This is the most important concept to understand.
- Different input: each time the recursive function is called it must be called with different data.
- Return: the recursive function should return a value.
What is Helper Method Recursion, and when is it commonly used?
A design pattern that uses two functions:
- an outer function that called to invoke the function, and
- an inner function (called helper function) which is a recursive function, and called by the outer function.
It is commonly used when needing to compile an array or a list of data.
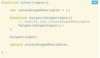
What is Pure Recursion?
A design pattern where the recursive function is totally self contained; so without the use of a nested or helper function.

What is Linear Search?
The simplest way to search for a value; look at every element in an array and check if it’s the wanted value.
What search method does JavaScript use on arrays for indexOf, includes, find, findIndex? What is the time complexity?
For these built-in array search methods, JavaScript uses a Linnear Search method. The time complexity is O(n).
When can one use Binary Search? What problem solving pattern does it use? What is its time complexity, and what is the advantage vs Linnear Search?
This search method only works on sorted arrays.
It uses the Divide and Conquer problem solving pattern; rather than eliminating one element at a time, it eliminates half of the remaining elements at a time.
It has a time complexity of O(log n) and it is a much faster for of search than for example Linnear Search with time complexity of O(n).
What are the 3 more elementary (simpler) and less efficient sorting algorithms? Why are they also known as quadratic algorithms?
These sorting algorithms are:
- Bubble Sort
- Selection Sort
- Insertion Sort
Their Big O time complexity is O(n²).
How does Bubble Sort work? What is its time complexity?
Sorting algorithm where on each iteration the larger value of an adjacent pair is swapped to the right, and as a result the largest value is “pushed” to the end of the array.
The array is sorted if no swap was made on an iteration.
The time complexity is: O(n^2)


