Algorithm concepts Flashcards
Uniform cost model
All machine operations have a constant cost, whatever the values
Time complexity
T(N) = aN + b
Asymptotic notation
aN + b = O(N) T(N) = O(N) highest order term determines the bound
Definition “Big O” (Upper Bound)
A function f(N) has an asymptotic upper bound given by the function g(N), written f(N) = O(g(N)), if and only if there are positive real numbers c and n0 such that 0 ≤ f(N) ≤ c g(N) for all N ≥ n0
Definition “Big Omega” (Lower Bound)
A function f(N) has an asymptotic lower bound given by the function g(N), written f(N) = Ω(g(N)), if and only if there are positive real numbers c and n0 such that 0 ≤ c g(N) ≤ f(N) for all N ≥ n0
Definition “Big Theta” (Tight Bound)
A function f(N) has an asymptotic tight bound given by the function g(N), written f(N) = Θ(g(N)), if and only if there are positive real numbers c1, c2, and n0 such that 0 ≤ c1 g(N) ≤ f(N) ≤ c2 g(N) for all N ≥ n0
Space complexity
The space complexity of an algorithm is the total amount of memory used, including that used by input parameters, as a function of the size of the input
Auxiliary Space
The auxiliary space is the amount of extra memory required, not including input parameters, as a function of the size of the input.
Polynomial
p(N) = a0 + a1N + a2N^2 + … + adN^d in which ad ≠ 0 asymptotically positive iff ad > 0
Exponential
include a term of the form a^N
Divide and Conquer
Recursion Tree
Master Method
Master Method pt 2
Master Method pt 3 (extra check)
Regularity condition
Master method excluded cases
The master method does not apply to these recurrences
T(N) = NT(N/2) + N T(N) = 0.5T(N/2) + 4N T(N) = 4T(N/8) − N2
T (N ) = 2T (N /2) + N / log N
The (mostly straightfoward) reasons are
the number of subproblems in the first two
negative divide and combine time (third example)
negative value of k (fourth example)
Heap
Binary search tree add code
Hash function
common to implement hash function in two steps
either stage can cause collisions
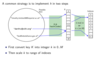
Adjacency lists
Code for Kruskal’s
Prim’s code
Bellman-Ford
Relax
Bellman-Ford to detect negative weight cycle
Bellman-Ford
Dijkstra
Dijkstra’s correctness
Dijkstra’s correctness pt 2
