algebraic methdos Flashcards
(20 cards)
how to prove by contradiction
- assume statement is false 2.conclude by saying that the original statement is true
rational number
a/b
irrational
cant be expressed as a/b
prove by contradiction that sqrt 2 is an irrational number

prove by contradiction that there are infinitely many prime numbers
https://www.youtube.com/watch?v=ZYkZws-23R8



note
Q= Irrational number
end the proof by saying what was said in the question
eg if question said “a+b is irrational”
then end it by saying “therefore a + b is irrational “


retarded proof question
(shows that most of it is just assuming differently and saying that this contradicts “said statement” that was first mentioned )


the following question from the retarded proof question


an example of going with your gut
( remember: contradiction questions can be answered by substitution methods )

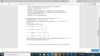
remember
rational numbers
have no common factors between them APART FROM 1
so if you prove that a and b have a common factor of twom you have proved that a/b is irrational therefore proving by contradiction that the statement is wrong

what do i do wrong when trying to prove that something is irrational ?
irrational numbers have common factors between them
(a/b)
when i find out that a^2= eg .. 2b^2 thus a is even,,,
i forget to say that since a is even, a = 2n
therefore 4n^2=2b^2
thus b^2=2n^2
since b^2 and a^2 have a common factor of 2 and the definition of a rational number is that both numbers dont have a common factor between them apart from 1, the fact that both have a common factor of 2 disproves that its rational, so now its infact IRRATIONAL !
note
the final statement has to contradict the ASSUMPTION!
WHAT do you do first before factorising?
factorise all fractions independently!
(also remember you can factor out whole numbers to make it easier !)

wo would you get partial fractions ?
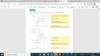
what would you do here?
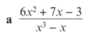
factorise the denominator!
MAKE SURE THAT THERE ARE NO POWERS IN THE DENOMINATOR!
(solve by substitution from here! )
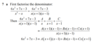
repeated factors !
eg
5/(x+2)^2
split into..
5/(x+2)^2 + 5/(x+2)
what do you do here ?

factorise- recognise that its a repeated factor
and do normal stuff
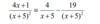
example of algebraic long division ?
and which how would you get the remainer
remember: the remainder is the number OUTSIDE of the bus stop thing



