Algebra with Radicals Flashcards
What does “like terms” mean when talking about radicals?
It means terms that have the same number under the root. For example:

What do you need to have in order to be allowed to add or subtract radicals?
You need “like terms” in order to add or subtract roots.
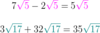
What if you want to add roots that are not alike?
For example:
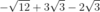
- Simplify the radical in each term
- Combine the like terms. (Add or subtract the numbers in front of the roots. The root portion doesn’t change.)
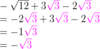
How do you simplify the following expression?
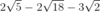
- Simplify the radical in each term (especially if the roots don’t all have the same number).
- Look for all of the terms that have roots with the same number.
- Add or subtract the numbers in front of the roots. (The root portion doesn’t change.)
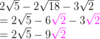
How do you simplify the following expression?
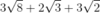
- Simplify the radical in each term (especially if the roots don’t all have the same number).
- Look for all of the terms that have roots with the same number.
- Add or subtract the numbers in front of the roots. (The root portion doesn’t change.)

What do you need to have in order to be allowed to multiply radicals?
Nothing.
Radicals and multiplication are best friends. You can willy nilly break apart and join together radicals via multiplying. (But don’t forget to simplify!)
How do you simplify the following expression?
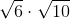
- Stuff all of the separate radicals into one. (Numbers inside the radical stay inside. Numbers outside the radical stay outside.)
- Simplify the radical.

How do you simplify the following expression?

- Stuff all of the separate radicals into one. (Numbers inside the radical stay inside. Numbers outside the radical stay outside.)
- Simplify the radical.
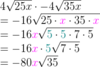
What do you need to have in order to be allowed to multiply radicals?
Nothing.
Radicals and division are also best friends. You can willy nilly break apart and join together radicals via division.
- Stuff all of the separate radicals into one. (Numbers inside the radical stay inside. Numbers outside the radical stay outside.)
- Simplify the fraction.
- Simplify the radical.
How do you simplify the following expression?
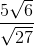
- Stuff all of the separate radicals into one. (Numbers inside the radical stay inside. Numbers outside the radical stay outside.)
- Simplify the fraction.
- Simplify the radical.
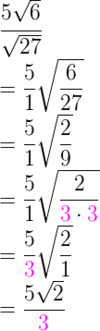
How do you simplify the following expression?

- Stuff all of the separate radicals into one. (Numbers inside the radical stay inside. Numbers outside the radical stay outside.)
- Simplify the fraction.
- Simplify the radical.



