Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

GMAT- Template > Algebra > Flashcards

Algebra Flashcards

1
Q

x = 3y - 2

10 - 2x = 8 - 3y

Solve for x and y using Substitution

A

We substitute the right side of the 1st equation in for “x” in the 2nd equation.

Make sure to use Parenthesis when doing substitution!

10 - 2(3y - 2) = 8 - 3y

10 - 6y + 4 = 8 - 3y

14 = 8 + 3y

6 = 3y

y = 2

Plug y = 2 back into 1st equation, to solve for x: x = 3(2) - 2 = 4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

What is a Quadratic Equation?

What is the General Form of a Quadratic Equation?

How would we put x2 - 3x = 2 into General Form, so we can factor it?

A

A Quadratic equation means that the variable is taken to the 2nd power.

Quadratics often have 2 solutions! Watch out– don’t assume only 1 solution!

The General Form is ax2 + bx + c = 0, where a, b, and c are constants

Subtract 2 from both sides:

x2 - 3x - 2 = 0

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

Factor x2 - 3x - 28 = 0

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

Solve by factoring:

x2 - x - 12 = 0

A

(x - 4) (x + 3) = 0

x = 4 or x = -3

To check, we can use FOIL:

F = First = x*x = x2

O = Outer = x*3 = 3x

I = Inner = -4x

Outer + Inner combines to = 3x - 4x = -x

L= Last = -4*3 = -12

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

Solve by factoring:

x2 + 10x = 0

A

Factor out an “x” from each term:

x(x + 10) = 0

x = 0 or (x + 10) = 0

x = 0 or -10

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

x2 = 25

x = ?

A

x = 5 OR -5

Remember to look for 2 solutions on Quadratics!

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

x2 = 2x

A

This is a “Disguised Quadratic”. It looks different from the General Form. However, it should be manipulated, factored, and solved as a Quadratic (which often gives 2 solutions).

x2 - 2x = 0

x(x - 2) = 0

x = 2 or 0

Common Error (we only get one solution. We miss the x=0 solution):

Divide both sides by x: x = 2

This is similar to the following error: x2 = 16, square root both sides, x = 4

OR, x = -4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

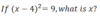
Factor x2 - y2

This is very common on GMAT. What do we call it?

A

Difference between Squares:

x2 - y2 = (x + y) (x - y)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Factor:

4x2 - 25

A

Difference between Squares:

(2x + 5) (2x - 5)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

Factor:

16x4 - 9y2

A

Difference between Squares:

(4x2 + 3y) (4x2 - 3y)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

Factor x2 + 2xy + y2

A

1: “Difference Between Squares”: x2 - y2 = (x + y) (x - y)

(x + y) (x + y) = (x + y)2

This results in only 1 solution, since it’s a perfect square.

These 3 Special Products are very common:

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

Factor x2 - 2xy + y2

A

1: “Difference Between Squares”: x2 - y2 = (x + y) (x - y)

(x - y) (x - y) = (x - y)2

This results in only 1 solution, since it’s a perfect square.

These 3 Special Products are very common:

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

Solve by factoring:

x2 + 9 = -6x

A

Add 6x to both sides: x2 + 6x + 9 = 0

(x + 3) (x + 3) = 0

Can also be written as (x+3)2 = 0

x = -3

Only 1 solution, because it’s a perfect square

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

Factor: a2b2 + ab = 2

Then, find b in terms of a

A

First, subtract 2 from both sides:

a2b2 + ab - 2 = 0

(ab + 2) (ab - 1) = 0

To check, we can FOIL:

F: ab*ab = a2b2

OI: ab* -1 + ab*2 = ab

L: 2*-1 = -2

To find b in terms of a: (ab+2) = 0 OR (ab - 1) =0

(ab+2) = 0, ab = -2, so b = -2/a OR

(ab - 1) = 0, ab = 1, so b = 1/a

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

What is |-10| ?

A

10

It turns a negative value into a positive.

Absolute value also means “distance from 0” on a number line.

| is the absolute value symbol.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

|x| = 4

What is x?

A

x = 4 or -4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

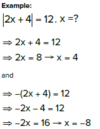
Data Sufficiency:

What is the value of x + 2y ?

(1) x + y = 2
(2) 6x + 12y - 3 = 15

A

(1) is Insufficient.
(2) is Sufficient.

We don’t always have to know both variables individually, when the question is asking for a combined value.

Watch out for the “C Trap”: when we think we need both statements, but one statement is sufficient.

We can manipulate (2), so that the left side is the same as the question:

Add 3 on both sides: 6x + 12y = 18

Divide by 6 on both sides: x + 2y = 3

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q
A
21
Q
A
22
Q

What is 4 squared?

A

4 squared = 42 = 4 * 4 = 16

4 is the base. 2 is the power.

For a power of 2, we use the word “squared”.

(This is because a square with 4 units on each side has an area of 42)

23
Q

What is 2 cubed?

A

2 cubed = 2 * 2 * 2 = 23 = 8

For a power of 3, we use the word “cubed”.

(This is because a cube with 2 units on each side has an area of 23)

28
Q
A
29
Q
A
30
Q

What “Perfect Square” less than 100 has 5 as a prime factor?

A

25 = 52

a Perfect Square is the square of an integer

For a perfect square, the prime factors have even exponents:

Examples: 36 = 22 * 32

100 = 22 * 52

31
Q

What “Perfect Cube” less than 100 has 3 as a prime factor?

A

33 = 27

a Perfect Cube is the cube of an integer

For a perfect cube, the prime factors have powers that are a multiple of 3.

Example: 1728 = 26 * 33 = (2*2*3)3 = 123

32
Q

23 * 24 = 2?

A

Multiplying Like Bases:

23 * 24 = 27

Add the powers:

xa * xb = xa+b

33
Q
A
34
Q

What is 0.33, as a fraction?

A
35
Q

xy-2 * x3y+5 = x?

A

xy-2 * x3y+5 = x4y+3

Multiplying Like Bases: add the powers

xa * xb = xa+b

38
Q

(x2)3 = x?

A

(x2)3 = x6

Power to a Power Rule:

(x<span>a</span>)<span>b</span> = xab

39
Q

a) What is x-1 ?
b) What is 2-3 ?

A

A negative exponent is the Reciprocal of the positive exponent:

(1 divided by the positive exponent)

40
Q

a) Express using a negative exponent
b) Express using a positive exponent

A
41
Q

If x-1 = 5, what is x?

A
42
Q
A

Square Root is the inverse of Squaring.

43
Q
A
44
Q
A
45
Q
A
46
Q
A
47
Q
A
48
Q
A
49
Q

0a = ?

A

0

0 to any power is 0.

50
Q

1a = ?

A

1

1 to any power is 1

53
Q

Is 0.43 > 0.42 ?

Why or why not?

A

No.

A fraction between 0 and 1 gets SMALLER as the power increases.

  1. 43 = 64/1000 = .064
  2. 42 = 16/100 = .16
54
Q

Is -(1/2)3 > -1/2 ?

A

Yes.

A positive fraction between 0 and 1, taken to greater power, gets closer to 0, and therefore smaller.

A negative fraction between -1 and 0, taken to an odd power,

is still negative and gets closer to 0, and therefore greater.

(-1/2)3 = -1/8

-1/8 > -1/2

55
Q

is a/b > (a/b)2 ?

(1) a < b
(2) a and b are positive

A

1) Insufficient. If a = 1 and b = 2, 1/2 > 1/4 –> Yes

If a = -1 and b=2, -1/2 < 1/4 –> No

(Note that a positive fraction between 0 and 1 gets smaller when raised to a higher power, but also we have to account for the possibility of a negative number)

2) Insufficient. If a = 1 and b = 2, 1/2 > 1/4 –> Yes

If a = 2 and b = 1, 2 No

Together: Sufficient. (2) rules out the negative number possibility that made (1) Insufficient

56
Q

Positive or negative?

a. (-1)5 ?
b. (-2)3
c. -32 ?
d. -3*(-4)7 ?

A

a. Negative. A negative number taken to an odd power is negative.
b. Negative.
c. Negative. Without the parentheses, we have to take the exponent first, before the - sign.

So, 32 = 9, and -32 = -9

d. Positive. (-4)7 is negative, so -3*(-4)7 is positive

GMAT- Template (13 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions