Algebra Flashcards
What is the Quadratic Formula?
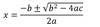
What is the general equation for Factorising the Difference of Two Squares (D.O.T.S.)?
x2-y2 = (x-y) (x+y)
= x2 + xy - xy - y2
= x2 - y2
What is the general equation for Factorising the Difference of Cubes?
x3 - y3 = (x - y) (x2 + xy + y2)
What is the general equation for Factorising the Sum of Cubes?
x3 + y3 = (x + y) (x2 - xy + y2)
How can you Factorise the Sum of Two Squares?
Hint: involves Imaginary numbers.
x2 + y2 = x2 - (-y2)
= x2 - (i2y2)
= x2 - (iy)2
= (x + iy) (x - iy)
What is the algebraic expansion of (a + b)2?
(a + b)2 = a2 + 2ab + b2
What is the algebraic expansion of (a - b)2?
(a - b)2 = a2 - 2ab + b2
Simplify aman
aman = am+n
Simplify am/an
am/an = am-n
Simplify (an)m
(an)m = anm
Simplify a0
a0 = 1
Simplify a1/n
a1/n = n√a
Simplify am/n
am/n = n√am
The log of a product is said to be equal to the sum of two logs.
Show what this means with relation to loga(xy)
loga (xy) = loga x + loga y
The log of a quotient is said to be equal to the difference of two logs to the same base.
Show what this means with relation to loga (x/y)
loga (x/y) = loga x - loga y
Simplify loga xn
loga xn = n•loga x
The rules of logs have a useful result when related to problems such as aloga of x
what is it?
aloga of x = x
inversely
x = aloga of x
The rules of logs have a number of obscure useful properties.
How can they be used to simplify the following?
axlogay
axlogay = yx
It is possible to change the base of a logarithm.
Show how using loga x
loga x = logb x / logb a
What does (a + b)3 expand to?
(a +b)3 = a3 + 3a2b + 3ab2 + b3
What does (a - b)3 expand to?
(a - b)3 = a3 - 3a2b + 3ab2 - b3


