AH 1.2 Angular Motion

Question 1

Explain what is meant by angular displacement (angle) by drawing a diagram and stating an equation.

Define all symbols used and specify units.

Answer 1

Question 2

State, in words, what is meant by angular velocity

Answer 2

Angular velocity is the rate of change of angular displacement.

Question 3

Write down the equation for angular velocity of a particle P describing uniform circular motion specifying all symbols and naming units.

Answer 3

Anglular velocity unit: radians per second

Angular displacemnt unit: radians

Time unit: seconds

Question 4

Write down the equation for instantaneous angular velocity.

Answer 4

Question 5

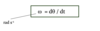
Write down the equation for instantaneous angular acceleration in terms of

anglular velocity and

angular displacement.

Answer 5

Question 6

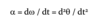
Copy and complete the table to show the angular versions of the linear equations of motion.

Answer 6

Question 7

Derive the equation given below for the linear (tangential) velocity of a body describing uniform circular motion.

Answer 7

Question 8

Derive the equation for the tangential linear acceleration of a body describing non-uniform circular motion.

Answer 8

Question 9

What condition must always be met for a body to describe iniform circular motion?

Answer 9

The body must be subjecy to a centrally directed i.e. centripetal force.

Question 10

Is a centripetal force always balanced or unbalanced?

Answer 10

Centripetal force always unbalanced.

Question 11

How is it possible for a body describing uniform circular motion to be accelerating whilst maintaining a constant linear speed?

Answer 11

Velocity is a vector quantity. Although the magnitude of the (linear) velocity is uniform, it’s direction is contstantly changing, as the object concerned is moving in a circle.

Question 12

Derive the equations for centripetal (i.e radial) acceleration given below.

Answer 12

Question 13

Answer 13

Question 14

Answer 14

Question 15

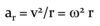
Study the information below then write down two equations for centripetal force. These follow directly from the equations for centripetal acceleration.

Answer 15

Question 16

See attached image for question.

Answer 16

See attached image for solution.

Question 17

A bucket of water on the end of a string is swung by a pupil in a vertical circle anticlockwise as you view it. This is showb below in the diagram.

Draw a digram showing all forces acting on the water at the following postions during the circular swing:

1) The top of the swing (12 o’clock position)
2) The bottom of the swing (6 o’clock position)
3) Half way up (3 o’clock position)
4) Half way down (9 o’clock position)

Answer 17

Question 18

A car of mass 800 kg travels at 20 ms^-1 round a circular road of radius 100m exhibit uniform circular motion.

Q1 What force causes the circular motion?

Q2 Find the size of this frictional force.

Answer 18

A1 A centrally directed Frictional force by the road on the tyres.

A2. mv²/r = f

f = 800 x (20²⁾ / 100

f = 3 200 N

Question 19

See attached image for question. In answering, consider ALL forces acting on the car in order to explain the cause of its circlar motion.

Answer 19

See attached image for solution.

Question 20

With the aid of a diagram, show that the linear speed v of a car describing uniform circular motion, radiud r, around a banked track, angle ø to the horizontal, is given by

v² = gr tan ø

What does this equation tell youy about the relationship between the angle of the track and the speed the car can go at in safely rounding the bend?

Answer 20

Question 21

Show that, for a car travelling at a uniform velocity v over a semi-circular arched bridge, radius r,

v = ⎷gr

Answer 21

Question 22

By sketching a concial pendulum and analysing the forces on the bob, show that the anlge ø of the pendulum string to the vertical is given by

tan ø = v²/gr

Answer 22