A2 & A3 Flashcards
(22 cards)
In a stochastic framework, explain why the Cape Cod method is preferred over the LDF method when few data points exist
Clark The Cape Cod method is preferred since it requires the estimation of fewer parameters. Since the LDF method requires a parameter for each AY, as well as the parameters for the growth curve, it tends to be over-parameterized when few data points exist.
Provide three advantages of using parameterized curves to describe loss emergence patterns.
Clark 1. Estimation is simple since we only have to estimate two parameters 2. We can use data from triangles that do not have evenly spaced evaluation data 3. The final pattern is smooth and does not follow random movements in the historical age to age factors
Briefly describe the two components of the variance of the actual loss emergence.
Clark Process Variance - the random variation in the actual loss emergence Parameter Variance - the uncertainty in the estimator
Provide two advantages of using the over-dispersed Poisson distribution to model the actual loss emergence.
Clark 1) Inclusion of scaling factors allows us to match the first and second moments of any distribution. Thus, there is high flexibility. 2) Maximum likelihood estimation produces the LDF and Cape Cod estimates of ultimate losses. Thus, the results can be presented in a familiar format.
Describe the key assumptions underlying the model outlined in Clark.
Assumption 1) Incremental losses are independent and identically distributed. Assumption 2) The variance/mean scale parameter is fixed and known Assumption 3) Variance estimates are based on an approximation to the Rao-Cramer lower bound
Briefly describe three graphical tests that can be used to validate Clark’s model assumptions.
Plot the normalized residuals against the following 3 variables. If the residuals for each graph are randomly scattered around zero with a roughly constant variance, we can assume the following: Incremental age - growth curve appropriate expected loss in each increment age - variance/mean ratio is constant calendar year - no calendar year effects
Briefly explain why it might be necessary to truncate LDFs when using growth curves.
Clark For curves with heavy tails (ex. loglogistic), it may be necessary to truncate the LDF at a finite point in time to reduce reliance on the extrapolation.
Compare and contrast the process and parameter variances of the Cape Cod method and the LDF method.
Clark Process variance - the CC method produces a higher process variance than the LDF method since it does not use a separate parameter for each AY. This leads to larger difference between expected loss emergence and actual loss emergence. Parameter variance - the CC method produces a lower parameter variance than the LDF method since it requires few parameters.
An actuary used maximum likelihood to parameterize a reserving model. Due to management discretion, the carried reserves differ from the maximum likelihood estimate. Explain why it may not be appropriate to use the coefficient of variation in the model to describe the carried reserve.
Clark Since the standard deviation in the MLE model is directly tied to the maximum likelihood estimate, it may not appropriate for the carried reserves.
An actuary used maximum likelihood to parameterize a reserving model. Due to management discretion, the carried reserves differ from the maximum likelihood estimate. Explain why it may be appropriate to use the coefficient of variation in the model to describe the carried reserve.
Clark Since the final carried reserve is a selection based on a number of factors, it stands to reason that the standard deviation should also be a selection. The output from the MLE model is a reasonable basis for that selection.
Briefly describe two problems with using the normal distribution as an approximation to the true distribution of R
If the data is skewed it is a poor approximation The confidence interval can have negative lower limits, even if negative reserve is not possible Mack 1994
To calculate the standard error of loss reserves using Mack’s method, we use the following formula:
One drawback of the formula above is that it does not provide an estimator for alpha(I-1)
Provide three options for calculating alpha(I-1)
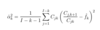
Mack 1994

Identify an alternative to normal distribution for R that avoids its problems
Lognormal Mack 1994
Provide three different variance assumptions for Cik.
Mack 1994

For each variance assumption, provide the formula for the corresponding estimator for fk and briefly describe the estimator in words.
Mack 1994

Describe a graphical variance test that can be employed in order to determine the appropriate fk estimator to use.
Mack 1994

The first implicit assumption underlying the chain-ladder method states that information contained in Ci,I+1-i cannot be augmented by using other Cik. Describe a major consequence of this assumption. In addition, briefly describe a procedure for testing this assumption.
- A major consequence is the assumption that development factors are uncorrelated
- To test this, we can run a statistical test where the test statistic is Spearman’s rank cor- relation. If our test statistic lies within a specified confidence interval around the true correlation, we fail to reject the null hypothesis that development factors are uncorrelated
Mack 1994
The second implicit assumption underlying the chain-ladder method states that accident years are independent. Describe a major consequence of this assumption. In addition, briefly describe a procedure for testing this assumption.
- A major consequence is the assumption that CY e↵ects do not exist
- To test this, we can run a statistical test to determine if diagonals exist where “small” development factors are prevalent (i.e. the development factors along the diagonal are smaller than usual). If our test statistic lies within a specified confidence interval around the true correlation, we fail to reject the null hypothesis that accident years are independent
Mack 1994
Briefly describe six testable implications of Mack’s chain-ladder assumptions.
Venter Factors
- Significance of the factor f(d) – the absolute value of f(d) should be at least twice its standard deviation for the factor to be considered significantly different from zero
- Superiority to alternative emergence patterns – use the sum of squared errors to determine which emergence pattern provides the best fit. Test statistics such as AIC and BIC could be used as well
- Linearity – plot incremental residuals against previous cumulative losses. If the points are randomly scattered around zero, we can assume linearity
- Stability – plot incremental residuals against time (i.e. AY). If the points are randomly scattered around zero, we can assume stability
- Correlation of development factors – calculate the sample correlation coecients for all pairs of columns in the development factor triangle. Count the number of significant correlations to determine if correlation exists
- Additive CY effects – use regression to determine if any diagonal dummy variables are significant. If so, then an additive CY effect exists and accident years are not independent
Briefly describe three alternatives to the standard chain-ladder emergence pattern.
Venter Factors
- Linear with constant – states that the next period’s expected emerged loss is a linear function of the previous cumulative losses PLUS a constant
- Factor times parameter – states that the next period’s expected emerged loss is a lag factor times the expected ultimate loss amount for an AY
- Factor times parameter including a CY effect – states that the next period’s expected emerged loss is a lag factor times the expected ultimate loss amount for an AY times a CY effect factor
Explain why the additive chain-ladder model and the Cape Cod model will always produce the same results.
Venter Factors
The Cape Cod model states that the next period’s expected emerged loss is a lag factor f(d) times the expected ultimate loss amount h. Since h does not vary by accident year, this is equivalent to the additive chain-ladder model which states that the next period’s expected emerged loss is a constant g(d) for all accident years. Thus, if we fit the Cape Cod model, we can define g(d) = f(d)h for the additive chain-ladder model. Similarly, if we fit the additive chain-ladder model, we can define f(d)h = g(d) for the Cape Cod model
Briefly describe three methods for reducing the number of parameters needed to fit the Bornhuet- ter/Ferguson model.
⇧ Assume several accident years in a row have the same mean level
⇧ Fit a trend line through the ultimate loss parameters
⇧ Group AY’s using apparent jumps in loss levels and fit a single h parameter to each group
Venter Factors


