A1. Formulae & Equations

Question 1

Pronumerals

Answer 1

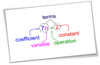
A pronumeral (or variable) is a letter in an equation or formula which represents a number.

Question 2

Like Terms

Answer 2

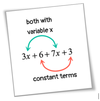
Like Terms contain the same pronumeral(s) and indices

• 3ab, 10ab and 2ba are like terms
• 5b² and -b² are like terms
• 3m² and 2m are unlike terms

Question 3

Collecting Like Terms

Like terms can be collected (added or subtracted)

[1] 3a² + 4a² =

[2] 5mn - 2nm =

[3] 2a + 3b =

Answer 3

Like terms can be collected (added or subtracted)

[1] 3a² + 4a² = 7a²

[2] 5mn - 2nm = 3mn

[3] 2a + 3b = 2a + 3b

Question 4

Indices and Index Laws
An index (or power or exponent) is used to abbreviate repeated multiplication.
Index Laws are rules for combing terms with indices.

Answer 4

Question 5

Multiplying Terms
Like or unlike terms can be multiplied.

[1] 3ab × 5c =

[2] 4ab × 2a²c =

Answer 5

When multiplying terms, multiply the numbers and then multiply the variables.

[1] 3ab × 5c = 15abc

When multiplying the same pronumerals ADD their indicies.

[2] 4ab × 2a²c = 8a²bc

Question 6

Dividing Terms

Like or unlike terms can be divided.

[1] 24abc ÷ 6ab =

[2] 15a⁵bc ÷ 3a²b =

Answer 6

Dividing Terms

When dividing terms, divide the numbers and then divide the pronumerals.

[1] 24abc ÷ 6ab = 4c

When dividing the same pronumerals, SUBTRACT their indicies.

[2] 15a⁵bc ÷ 3a²b = 5a³c

Question 7

Raising Powers to Powers

• (2a⁵b²)³ =

Answer 7

When raising terms with powers to powers, MULTIPLY the powers.

• (2a⁵b²)³ = 2³a¹⁵b^{<span>6</span>} = 8a¹⁵b^{<span>6</span>}

Don’t forget to raise the constant term in the brackets to the power as well.

Question 8

Expanding Brackets

Expand 4(b + 6)

Answer 8

Expanding brackets means removing the brackets (grouping symbols) by multiplying each term inside the brackets by the term outside of the brackets.

Question 9

Formula

Answer 9

A formula is a rule that describes a relationship between 2 or more variables.
The variable on the LHS is callled the SUBJECT of the formula.

Question 10

Formula Applications - Medicine Dosage

The correct dosage of medicine for infants (babies up to 2 years) depends on the child’s age or weight.

Answer 10

Fried’s, Young’s or Clark’s rules can be used to convert an adult dosage to a child’s dosage. These formulas when required will be provided in the question.

Question 11

Solving Equations

Solving equations require a series of ‘undo’ operations.

• Subtraction undoes _______
• Addition undoes _______
• Multiplication undoes _______
• Division undoes _______
• Square rooting undoes _______
• Squaring undoes _______

Answer 11

• Subtraction undoes Addition_
• Addition undoes Subtraction
• Multiplication undoes Division
• Division undoes Multiplication
• Square rooting undoes Squaring
• Squaring undoes Square Rooting

Question 12

Two Step Equations

A 2-step requires two ‘undo’ steps to solve.

Answer 12

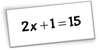
• Show all ‘undo’ steps on both sides of equation.
• Check answer by subsitution.

Question 13

Equations With Brackets

Answer 13

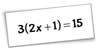
First step - expand all brackets by multipllying each term inside the brackets by the term outside of the brackets.

Question 14

Equations With Fractions

Answer 14

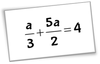
First Step - eliminate fractions by multiplying EVERY term on both sides of the equation by the lowest common multiple of the denominators.

Question 15

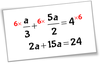
Equations With Pronumerals on Both Sides

Answer 15

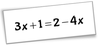
First Step - move the smallest pronumeral term first.

Question 16

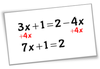
Formulas & Equations

Sometimes after a value is subsituted into a formula the result is an equation which must be solved.

Answer 16

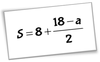
Find the value of a if S = 14.

Question 17

Changing the Subject

Some formulas can be rearranged to make another variable the new subject of the formula.

Answer 17

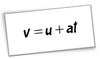
To change the subject use the same ‘undo’ steps as for solving an equation.

Question 18

Speed, Distance & Time

Answer 18

Question 19

BAC Formulas

The Blood Alcohol Content is the concentration of alcohol (in mg) per 100 mL of blood.

Answer 19

Different formulas are used to calculate BAC in males and females because of their different body builds.

Question 20

Returning BAC to Zero

A normal body can only reduce the BAC by about 0.015 to 0.020 per hour.

Answer 20

Question 21

Converting Units of Speed

It is necessary to convert speed measured in km/h into m/s to calculate Reaction Time Distance.

Answer 21

1 hour = 60 × 60 s = 3600 s

Question 22

Reaction Time Distance

Answer 22

Reaction Time Distance is the distance a car travels in the time between the decision to stop and applying the brakes.

Use Distance = Speed × Time

Question 23

Braking Distance

Answer 23

Braking Distance is the distance a car travels before coming to a stop after the brakes have been applied. Using the braking distance formula usually involves finding the value of the constant k.

Question 24

Stopping Distance

Answer 24

Stopping distance is the sum of the Reaction Time Distance (RTD) and the Braking Distance.