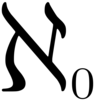A Fraction Ahead Review Flashcards
This deck of flash cards will review some of the topics covered during A Fraction Ahead, along with some extras
In geometry, what does congruent mean?
Two shapes that are identical in every way
What is a regular polygon?
A polygon whose side lengths are all equal, and whose angles measurements are all equal
What is a Platonic solid?
A 3 dimensional shape whose faces are congruent regular polygons, with the same number of faces meeting at each vertex
How many Platonic solids exist, and what are their names?
5: Tetrahedron, Cube, Octahedron, Dodecahedron, Icosahedron
What shapes are the faces of a tetrahedron, and how many faces does a tetrahedron have?
Triangles with 4 faces
What shapes are the faces of a cube, and how many faces does a cube have?
Squares with 6 faces
What shapes are the faces of an octahedron, and how many faces does an octahedron have?
Triangles with 8 faces
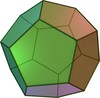
What shapes are the faces of a dodecahedron, and how many faces does a dodecahedron have?
Hexagons with 12 faces
What shapes are the faces of an icosahedron, and how many faces does an icosahedron have?
Triangles with 20 faces
What are some of Plato’s most popular philosophical ideas?
What is the formula for the addtion of numbers from 1 to a natural number n?
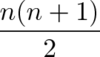
How do you derive the formula for the addtion of numbers from 1 to a number n?
What symbol is used to describe a factorial?
!
How do you calculate a factorial?
Multiply each number in descending order up until 1. Example: 4! = 4x3x2x1 = 24
What does a factorial tell us?
How many ways you can order a certain amount of objects
How many ways can you order a deck of cards?
52! ways, or approximately 8.0658175e+67 ways
Is 52! a large number?
Yup
Just how big is 52!?
If the video starts at the beginning, the explanation starts about 14 minutes in.
What is this symbol called, and what does it represent?
It is a “blackboard bold” N, and it represents the set of natural numbers
Which numbers are included in the set of natural numbers?
{1, 2, 3, 4, …}. The “…” means this goes on forever. Some mathemeticians include 0 in the natural numbers.
What does this symbol represent?
The set of integers
Which numbers are contained within the set of integers?
{…, -2, -1, 0, 1, 2, …}
What does this symbol represent?
The set of rational numbers
Which numbers are included in the set of rational numbers?
Any number (positive or negative) that can be represented as a fraction / ratio
What does this symbol represent?
The set of real numbers
Which numbers are included in the set of real numbers?
All of the rational numbers and all of the irrational numbers
What is an irrational number?
A number that cannot be represented by a ratio of integers. Their decimal expansions never end and never repeat
What are some examples of irrational numbers?
π, e, the square root of any number that cannot be represented as a ratio of perfect squares, and many more
What is a perfect square?
A number that can be found by multiplying 2 of the same integers. Examples: 4 (2*2), 9 (3*3), 100 (10*10), etc
What is this symbol called and what does it represent?
Aleph Null, it is the cardinality of a countably infinite set (such as the sets of natural numbers, integers, and rational numbers)
What is cardinality?
The number of elements in a set. For example, the cardinailtiy of the set {apple, pear, orange} is 3, because it contains 3 elements
In regards to set theory, what is an element?
What is a set?
A collection of elements contained within curly brackets. Example: Set A = {3, 4, red, 9, banana}
What is a union of 2 sets?
The combination of 2 sets into 1 set, without any repetitions. Example: Set A = {1,5,7} and Set B = {2,5,7,8,10}
The union of set A and B is: A∪B = {1,2,5,7,8,10}
What is the intersection of 2 sets?
Creating a new set with shared elements of 2 sets. Example: Set A = {1,2,3} and set B = {2,3,4}.
The intersection of sets A and B is: A∩B = {2,3}
What is the empty set?
A set containing no elements, denoted by the symbols ∅ or {}
What is the complement of a set?
A set containing all elements that are not in the specified set but are in the universe of numbers that are being worked with.
Example: There exists a set A = {-1,0,1} in ℤ. The complement of set A would be: Ac = {…, -3, -2, 2, 3, …}
What is the name of this mathematical tool?
The Cartesian plane / coordinate plane
What was the name of the mathematician / philosopher who invented the Cartesian plane?
René Descartes
Which two branches of math does the Cartesian plane unify?
Algebra and Geometry
What is the name of this method that approximates the area under a curve?
Riemann Approximation Method
What calculus operation is used to find the area under a curve?
The integral
