3.3 - Graphs

Question 1

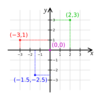
I can plot points (x, y) in any of the four quadrants of a graph

For example, I can plot (2, 3), (-3, 1), (0, 0) and (-1.5, -2.5)

Answer 1

Question 2

I can workout the midpoint of a line segment, given its endpoints

For example, if a line segment goes from (5, 10) to (-3, 6), its midpoint is…

Answer 2

(1, 8)

Question 3

I can read a straight line graph to convert between two units

For example, given the following graph, how many Euros is 7 pounds?

Answer 3

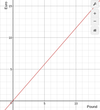
8 euros

Question 4

I can find the gradient of a straight line

For example, what is the gradient of this line?

Answer 4

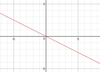
gradient = (increase in y) ÷ (increase in x)
         = -4 ÷ 2
         = -0.5

Question 5

I can find the gradient of a straight line given the coordinates of two points

For example, what is the equation of the straight line through (1, 7) and (2, 9)?

Answer 5

gradient = (increase in y) ÷ (increase in x)
          = 2 ÷ 1
          = 2

calculate the intercept by substituting into y = mx + c

y = mx + c
7 = 2 × 1 + c
7 = 2 + c
c = 5

Equation of the line: y = 2x + 5

Question 6

Given one line, I can find the gradient of another perpendicular line

Answer 6

If the gradient of the first line is m, then the gradient of the second line is -1 ÷ m

Question 7

I know what the equation of a line is

Answer 7

y = mx + c

• m is the gradient of the line
• c is the point where the line crosses the y-axis.

Question 8

What is the equation of the straight line with gradient 6 that passes through the point (0, 2)?

Answer 8

y = 6x - 2

Question 9

What does the line x = 5 look like?

Answer 9

A vertical line passing through (5, 0)

Question 10

What does the line y = 3 look like?

Answer 10

A horizontal line passing through (3, 0)

Question 11

What does the line y = x look like?

Answer 11

A diagonal line with gradient 1, passing through (0, 0) and (1, 1)

Goes from bottom left to top right.

Question 12

What does the line y - x = 0 look like?

Answer 12

A diagonal line with gradient -1, passing through (0, 0) and (1, -1)

Goes from top left to bottom right.

Question 13

Given a formula, I can plot a graph

Answer 13

Draw out a results table for different values of y:

y | 0 | 1 | 2 | 3 | ...
x | 2 | 4 | 8 | 16 | ...

Plot the points on a graph, and join up with a curve

Question 14

Given a graph of y = f(x), I can sketch y = f(2x)

Answer 14

It will be squashed in the horizontal direction, so each point is half as far from the y-axis

Question 15

Given a graph of y = f(x), I can sketch y = 2f(x)

Answer 15

It will be stretched out in the vertical direction, so each point is twice as far from the x-axis

Question 16

Given a graph of y = f(x), I can sketch y = 2 + f(x)

Answer 16

It will be shifted two up

Question 17

Given a graph of y = f(x), I can sketch y = f(x + 2)

Answer 17

It will be shifted two to the left

Question 18

I can estimate the gradient of a non-linear graph

Answer 18

Draw a tangent at the point you are interested in (with a ruler)

Calculate the gradient of the tangent like any other straight line

Question 19

I can look at the intersections of lines to solve complex equations

For example, this is a graph of y = x + 4/x - 3

How would you use it to solve the equation 5x + 4/x - 3 = 0?

Answer 19

• Rearrange the equation so that it contains the equation of the graph:

0 = 3x + 4/x + 13
 0 = ( x + 4/x - 3) + 2x - 10

• Substitute in y and rearrange to put y on the left

0 = ( x + 4/x - 3) + 2x - 10
 0 = y + 2x - 10
 y = -2x + 10

• Draw this new line
• The x-coordinates where the two lines intersect show the solutions

Question 20

Given one line, I can find the gradient of another parallel line

Answer 20

They will be the same