13. Conic Sections Flashcards
(14 cards)
Forming a Parabola
The plane is parallel to a lateral edge of the cone.
Forming a Hyperbola
The plane is parallel to the axis of the cone.

Forming an Ellipse
The plane is neither parallel to a lateral edge nor the axis of the cone.

Definition of a parabola
The set of points that are equidistance from a given point (focus) and a given line (directrix). The center of a parabola is its vertex.

If a parabola has an x-orientation…
- It opens to the left (p<0) or right (p>0)
- The standard equation is (y–k)2 = 4p(x–h)
- The focus is (h+p, k), and the directrix is x = h–p
- The vertex is (h, k)
- The common distance from the parabola to the focus and directrix is |p|
If a parabola has an y-orientation…
- It opens up (p>0) or down (p<0)
- The standard equation is (x–h)2 = 4p(y–k)
- The focus is (h, k+p), and the directrix is y = k–p
- The vertex is (h, k)
- The common distance from the parabola to the focus and directrix is |p|
Definition of an ellipse
The set of points whose distances from two given points (foci) sum to a constant.
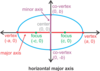
If an ellipse has an x-orientation…
- The standard equation is (x–h)2/a2 + (y–k)2/b2 = 1, where a2 > b2
- The major axis is parallel to the x-axis
- The center is (h, k)
- The vertices are (h–a, k) and (h+a, k), the endpoints of the major axis. So the major axis is 2a long.
- The endpoints of the minor axis are (h, k–b) and (h, k+b). So the minor axis is 2b long.
- The foci are on the major axis. Each focus is at a distance of c = √(a2–b2) from the center, so the foci are at (h–c, k) and (h+c, k).
If an ellipse has an y-orientation…
- The standard equation is (x–h)2/b2 + (y–k)2/a2 = 1, where a2 > b2
- The major axis is parallel to the y-axis
- The center is (h, k)
- The vertices are (h, k–a) and (h, k+a), the endpoints of the major axis.
- The endpoints of the minor axis are (h–b, k) and (h+b, k).
- The foci are on the major axis. Each focus is at a distance of c = √(a2–b2) from the center, so the foci are at (h, k–c) and (h, k+c).
Definition of a hyperbola
The set of points whose distances from two fixed points (foci) differ by a constant. A hyperbola has two halves, corresponding to the two nappes of the cone.
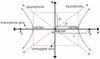
If a hyperbola has an x-orientation…
- The hyperbola opens to the sides.
- The standard equation is (x–h)2/a2 – (y–k)2/b2 = 1.
- The center is (h, k).
- The vertices are (h–a, k) and (h+a, k). The segment joining the two vertices is called the transverse axis. This axis is horizontal and has length 2a.
- The foci are on the transverse axis. The distance between the center and each focus is c = √(a2+b2), so the foci are (h–c, k) and (h+c, k).
- The vertical segment through the center with endpoints (h, k–b) and (h, k+b), which has length 2b, is called the conjugate axis. The endpoints of this axis are not on the hyperbola.
- The equations of the asymptotes are y–k = ±b/a(x–h).
If a hyperbola has a y-orientation…
- The hyperbola opens up and down.
- The standard equation is (y–k)2/a2 – (x–h)2/b2 = 1.
- The center is (h, k).
- The vertices are (h, k–a) and (h, k+a). The transverse axis is vertical and has length 2a.
- The foci are (h, k–c) and (h, k+c).
- The conjugate axis is horizontal, has endpoints (h–b, k) and (h+b, k), and has length 2b.
- The equations of the asymptotes are y–k = ±a/b(x–h).
Eccentricity of an ellipse or hyperbola
The measure of its degree of elongation.
The eccentricity is c/a.
Standard equation of a circle
(x–h)2 + (y–k)2 = r2
with center at (h, k) and radius = r


