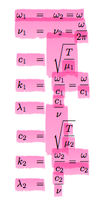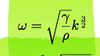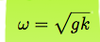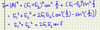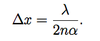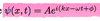1224 Flashcards
How do you sum 2 oscillations with same frequency to find amplitude?
Use complex notations
What is the resultant/carrier/average frequency?
ω1 + ω2/2 or f1 + f2/2
describes net motion
What is envelope/modulation frequency?
ω1 - ω2/2 or f1 - f2/2
describes wave motion
What happens when frequency are similar for same amplitude and same phase oscillations? What is the frequency of the phenomenon?
beats i.e. oscillation at amplitude of resultant frequency is modulated by slow oscillation at envelope frequency
ω1 - ω2 or f1 - f2/2
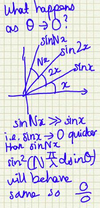
What is the number of minima per second for beats?
Δω/π
where Δω = envelope frequency
What is the frequency for Ψ1 +Ψ2 in normal modes? And what is the frequency for Ψ1-Ψ2?
What is the general wave equation?
What are the speeds and impedances for stretched string, elastic waves and fluids in waves? And assumptions for derivation of the stretched string equations?
Small displacement of strings
T and u are independent of posn and displacement
Resolved force has small angle between x and x + Δx
What are the reflection coefficients and transmission cofficients? And what happens for z1 >> z2, z2 >> z1 and z1 = z2?
- z1 >> z2 => R=1 & T=0 => no phase change
- z1 << z2 => R=-1 & T=0 => pi phase change
- z1 = z2 => R=0 & T=1 => impedance matching like as if only one string
Define impedance as equation and in words.
Impedance is measure of resistance to oscillations (amplitude of driving force/transverse velocity)
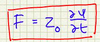
What is the phenomenon when source is moving faster than velocity of waves in medium?
Shock waves
What is the kinetic energy density of a string? And what is the equation in terms of speed and impedance?
KE = 1/2 u (dΨ/dt)^2
What is potential energy stored in string? And what is total energy per unit length?
U (x,t) = potential energy
What is the most general solution to the wave solution?
How do you sum 2 oscillations with same frequency to find angle?
What is correponding defined qa and qb variables?
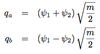
What is the rate at which energy moves along wave (i.e. power delivered along string) = rate at which is done?
What is the instantaneous KE & PE densities of any point on string under tension carrying travelling wave?
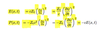
Define harmonic
integer multiple of fundamental frequency
What are the boundary conditions for string of length L fixed at both ends?
What is fundamental frequency?
Lowest resonant frequency of a vibrating object i.e. 1st harmonic
What is another general solution to general wave equation involving k? Why can you do this
Scaling x by a constant does NOT change wave velocity
Also kx+wt (or kx-wt) = phase
What are the conditions to drive a wave along a semi-infinite string?
- Driver must apply force proportional to transverse velocity at end of string it is driving
- constant of proportionality = characterisitc impedance
What is the condition to terminate a finite driven string?
Must be terminated with impedance equal to characteristic impedance of string (in order to have same wave motion as that on an infinite string)
What happens if string is not terminated with correct impedance?
Reflection and transmission will occur according to their coefficients
What is true at the junction between 2 strings of different mass per unit length (but under same tension)?
Send wave with frequency ω down 1st string then all points on string will oscillate harmonically with frequency ω => excite waves of same frequency in 2nd string
How do you solve the wave equation using function as a single variable u= x-ct?
Give the boundary conditions for pipe with both open ends, closed ends and one opened & one closed. Explain the conditions. (The pressure nodes ones)
- Pressure is fixed by surrounds => pressure is a node
- Change in pressure (p) is given by the picture
- Pressure is pi/2 out of phase with displacement
- Ψ (x=0) = Ψ (x=L) = 0 for both closed ends
Explain the difference between KE of source and KE of source as measured by observer (involves Doppler effect).
Define sound level and inverse square law of sound.
Derive Doppler shifts for moving observer and both source and observer moving towards each other.
Define group and phase velocity. Also what one propagates energy and information?
- Group velocity (envelope) gives energy and info
What are the conditions for non-dispersive waves?
- Group velocity = phase velocity
- ω = ck
- shallow water when ω=sqrt(ghk) since speed of water decreases as water gets shallower
Sketch wavepacket showing group and phase velocity.
What are the assumptions about water?
- Hard to compress
- Low viscosity
What are the 2 regimes for water waves and their conditions?
- Deep water kh >> 1 (then tanh(kx) → 1)
- Shallow water kh << 1 (then have to expand tanh(kx))
What is the dispersion relation?
- relationship between group and phase velocity
What is the dispersion relation for deep water when λ is small (ripples)?
What is the dispersion for deep water at long λ? And what are these waves?
- Gravity waves
- group velocity < phase velocity
- dispersion does not contain density hence will hold for any non-viscous incompressible fluid
What is the dispersion relation for shallow water at small values of hk?
- expression from tanh(kh) expansion around 0 is simplified further to eqn in picture
- these waves are dispersionless
What happens as shallow water gets shallower?
- depth of water (h) decreases so group and phase velocity decreases
- amplitude increases to conserve E (since E = KE + PE)
- so PE increases due to increasing amplitude to keep E constant
- e.g. waves breaking at sea-shore or tsunami
What happens at small λs and large λs for water waves due to the 2 restoring forces from surface tension (flatten out) and gravity (water piled up in crests to fall under gravity)?
- small λs => surface tension γ dominates
- large λs => gravity g dominates
Explain how a Fabry-Perot etalon works and produces sharp bright fringes.
- large number of multiple reflected rays (could be infnite but amplitude between successive wave decreases) between 2 partially silvered plates [higher number of interfering light sources = better resolution]
- which are out of phase by a constant increment - constant path diff. of mλ (2tcosθ=mλ) [pi phase change at each mirror hence no overall phase change]
- increases sharpness of inference max. => bright fringes
- interference fringes focussed by convering lens => concentric circles
What are Fraunhofer limit and conditions?
- light approaching diffracting object is parallel & monochromatic (interfering light rays are II to each other)
- screen is at distance much larger compared to size of diffracting object
- dsinθ=mλ
What is Rayleigh’s criterion?
- 2 wavelengths are just resolved when max. of one lies at 1st min. of the other
- θr=λ/a
- for circular aperature: θr = 1.22λ/D (D=diameter of circle)
How does Michelson interferometer work?
- interference pattern of recombined beams that have travelled a different distance d=Lf-Lm
- hence altering posn of movable mirror => control path diff.
- path diff. = 2Δ which equals 2ndcosθ (so Δ=ndcosθ)
- pi shift in beam that strikes fixed mirror (reflection from back of beam splitter) & approximate nair = 1 hence bright fringes when 2dcosθ = (m+0.5)pi
- [light strikes mirrors at angle θ to normal)
What is the purpose of compensator plate in Michelson interferometer?
- to add a λ-dependent phase diff. since path diff. in glass for each beam may not be the same if use light of different λs and nglass is slightly λ dependent
- compensator plate have same thickness & material as beam splitter
- also to make sure beams travel through beam splitter twice each
Derive intensity of Michelson interferometer if beam is split into 2 equal amplitude.
- use (kx-wt) where x is distance travelled by light
- for movable mirror, light travels 2Lm
- for fixed mirror, light travels 2Lf= 2Lm+2Δ
- take out exponentials as common factor since exp(ix)e(-ix)=1
When is intensity max, min and 1/2 for Michelson interferometer?
- d increases => cosθ decreases => θ for same fringe (same m) increases
- expand outwards & new fringes appear at centre => ring appear from centre and expand
What is a wavefront?
What is a ray?
The plane of constant phase (and amplitude?) on a wave.
The normal to the wavefront.
Define the refractive index.
Define optical path length.
refractive index, n =c/v
Optical path length (OPL) = nΔx
State Fermat’s theorem.
Fermat - Light, in going between two points, traverses the
path with the smallest optical path length.
State Huygen’s principle.
Huygen - Every point on a wavefront acts as a point source for secondary wavelts propagating radially outward, such that at a later time, the primary wavefront is the envelope of the secondary wavelets.
State Snell’s law.
What is the critical angle?
For light travelling from high to low refractive index, the angle of refraction must be greater than the angle of incidence. The largest possible value for refraction is pi/2, which corresponds to the maximum angle of incidence for refraction to occur. Beyond this angle, there are no real angles that satisfy the equation:
.
Beyond this angle, total internal reflection occurs (TIR).
What is linearly polarised light?
Light whose plane of vibration has a fixed orientation.
The electric field vector is confined to a given plane along the direction of propagation.
State the law of malus.
What is the intensity of unpolarised light transmitted when passed through a linear polariser?
If we have plane polarised light incident at an angle to the plane of polarisation of a perfect polariser, onl the componet of the field along the direction of the transmision axis is transmitted.
Half the intensity of natural light is transmitted since light has components travelling in all directions.
What is circularly polarised light and how is it produced?
Light with constant amplitude whose plane of vibration rotates in time. If rotation is clockwise - right-circularly polarised light, if anticlockwise - left-circularly polarised light.
It can be produced by obtaining linearly polarised light whose orthogonal components (i.e. x and y) have equal amplitudes and either advancing or delaying one component by pi/2.
E = E0 cos(kz − ωt)i + E0 sin(kz − ωt)j.
How is circular polarisation used in 3D glasses?
Circular polarisers are used in 3D cinemas
where the film is shown in the two polarisations and glasses receive one type of
circular polarisation in one eye and the other type in the other eye. If glasses
with linear polarisers were used the wearer would have to keep their head at
exactly the right orientation so that one eye would continually receive just one
polarisation and the other eye the other. Tilting would cause a mixture to be
observed in each eye
What is elliptically polarised light?
Similar to cicular polarisation, except the orthogonal components (x and y) do not have equal amplitudes and they do not have to be pi/2 out of phase. For this reason, linear and circular polarisations are special cases of elliptical polarisation with linear having theta = 0 and circular having the amplitudes equal and theta = 90.
Fresnel’s equations
Fresnel’s Equations:
What is Brewster’s angle?
At one particular angle of incidence, the component of the field parallel to the plane of incidence is entirely transmitted with its reflection coefficient going to zero. This possible because:
Amplitude-phase curve from lower to higher refractive index.
Amplitude-phase curve from higher to lower refractive index.
Reflection coefficient (%)-a ngle of incidence - low to high refractive index
Reflection coefficient-phase - high to low refractive index
Notice that brewster’s angle is still there but no critical angle.
Name the methods of polarisation and provide a very brief description of each.
- Reflection - There is a preferential reflection of light polarised perpendicular to the plane. This is entirely the case at brewster’s angle.
- Absorption - Some crystalline materials absorb more light in one direction than another. This anisotropy is called dichroism.
- Birefringence - Crystalline materials may have different indices of refraction associated with
different directions. - Scattering - Light scattering of molecules causes oscillations perpendicular to the direction of travel of light. Light travelling along z causes oscillations in x and y, therefore the nuclei/charges oscillating in x/y will radiate in y/x.
What happens when you put an object of thickness t and refractive index n into 1 arm of Michelson interferometer?
- increase path diff. by 2t(n - nair) since light travels in both directions in each arm hence goes through object twice
- correponds to 2t(n - nair)λ wavelengths => phase shift that corresponds to wavelength shift as well
- pattern changes by 2t(n - nair)λ fringes
- (imagine moving along sin curve, object introduced shift is past pi/2 so add pi/2 to get overall intensity)
How do you calculate intensity for Fabry Perot etalon?
- consider amplitude of each successie transmitted beam
- I is given by I=Imax(1/1+Fsin^2γ) where F=4R/(1-R)^2
- max. amplitude when I=Imax i.e. when sinγ=0 so this happens for γ=m*pi
What is the lowest order fringe for Fabry Perot etalon? Why?
- m=1
- since at m=0, no fringe because it’s at right angles to etalon where no light is transmitted
How do you find the chromatic resolution for Fabry-Perot etalon for λ2 - λ1 = Δλ?
- condition: max. of one coincides with HALF max. of the other (since intensity never becomes 0)
- hence need distance between 1/2 Imax and I max for one wavelength (consider γ at 1/2 and let γ=γmax +Δγ => use double angle formulae and the fact that you know what sinγmax and cosγmax => use small angle approximation)
- then find 2 formulas for Δcosθ by when λ & t are fixed and when m & t are fixed
What is path diff. between 2 parallel rays for Young’s double slit? Prove it
- dsinθ=mλ where θ=angle normal to interfering light rays
- consider distance travelled by r1 and r2
- OPD = r2-r1 => use Pythagoras to find them
- take out L as a common factor so eqn is in form for binomial expansion since ASSUMED that L >> (y+d/2) or (y-d/2) so (y+d/2)/L << 1 or (y-d/2)/L << 1
- y/L=tanθ => use small angle approximation so tanθ=sinθ
How do you find intensity for Young’s double slit with equal amplitude? Hence when is intenisty max, 1/2 and 0?
- consider distances travelled by r1 and r2 => in the case of r2, it travels r1+dsinθ (note: δ is kdsinθ)
- put out a factor of exp(ikr1 +iδ/2)
- max. when δ/2=m*pi
- 0 when δ/2=(m+0.5)*pi
- 1/2 when δ/2=(m+0.75)*pi or (m+0.25)*pi
What happens if a block of thickness t and refractive index n is placed in front of one of the slits?
- d→nd and λ→λ/n
- adds path diff. (n-1)t => fringe shifted
- IF (n-1)t=λ/2 => corresponds to phase shift of pi between 2 beams hence points of bright fringes become dark fringes
Under what conditions can the Fraunhofer limit breakdown?
- path. diff becomes large ( m>>1) => coherence lost so fringe pattern starts to degrade
- y becoming larger => also affects pattern
What is coherence?
Define spatial and temporal coherence.
Coherence: A measure of how well a real wave approximates an infinite plane wave.
Spatial - The distance over which the relationship Δφ=kΔx is valid.
Temporal - The time over which the relationship Δφ=ωΔt is valid.
What is the intensity if amplitude from slits are unequal in Young’s double slit diffraction? When is intensity max and min?
- same with equal amplitude, take out factor of exp(ikr1+iδ/2)
- Then write exponentials in terms of cos and sin
- Then group together terms with cos and sin
- max. when δ/2=m*pi [I is proportional to (E1+E2)^2)]
- 0 when δ/2=(m+0.5)*pi [I is proportional to (E1-E2)^2)]
- i.e. same conditions for equal amplitude waves
Why do you need fringe visibility (V) when the amplitudes are unequal in Young’s double slit?
- since Imax and Imin depends on amplitude hence if sufficiently different fringes may be hard to see
- V needs to be greater than some value for reasonable clarity
What is the optical path difference in thin-film interference?
What is diffraction grating? And what is the intensity?
- array of N slits (equally spaced) => path diff. between successive rays is dsinθ
- calculate total amplitude using same method as double slit except you have a geometric series
- but still take out common factors like exp[iNδ/2] and exp[iδ/2]
What are the conditions for phase changes upon reflection?
- High to low refractive index - 0 phase change
- Low to high refractive index - π phase change
What happens to intensity when x=(π/λ)dsinθ and x→0? And when is there a primary max., min and subsidiary max.?
- x→0 => sinx = x (small angle approximation) hence I → I0N2
- primary max. when sin2((π/λ)dsinθ) = 0 => π/λ)dsinθ=mπ i.e. dsinθ=mλ
- min. when sin2((Nπ/λ)dsinθ)=0 i.e. (Nπ/λ)dsinθ=kπ (k = another integer) EXCEPT in cases where k/N=m => primary max. (since denominator is also 0) hence k≠Nm for zeros
- subsidiary max. when sin2((Nπ/λ)dsinθ)=1 i.e. (Nπ/λ)dsinθ=(m+0.5)π
Thin-film interference
Soap film
Thin-film interference
Oil film
Thin-film interference
Anti-reflection coating
Why do you get more maxima at lower λ for a given theta in diffraction grating?
- dsinθ=mλ (condition for primary max.)
- λ decreases → m increases for fixed theta
- => λblue will have more maxima than λred => can use diffraction grating to resolve spectral lines like Fabry Perot
Derive chromatic resolution of 2 wavelengths (λ1 & λ1+Δλ) where Δλ<<λ1 diffraction grating.
- condition: resolved if primary max. of one coincides with min. of other
- consider change in angle from primary max. to 1st zero and how maxima posn changes as λ changes
- primary max when dsinθ=mλ
- zero when dsinθ=(k/N)/λ EXCEPT when k/N=m => so let k=mN+1 for 1st zero hence dsinθ=(m+1/N)/λ
- so for fixed λ change from max. to 1st zero is dΔsinθ=λ/N => Δsinθ=λ/Nd
- how max. posn changes as λ changes (fixed m): dΔsinθ=mΔλ => Δsinθ=mΔλ/d
- equate two expressions for Δsinθ => λ/Δλ=mN
What is the optical path difference for light passing through a wedge?
What is the fringe separation?
Remember that the distance d is almost the same in the case of a very small angle, and that the small angle approximation for d = x tan α ≈ αx is used.
What are the conditions for minima and maxima for a thin wedge and why must this be true?
Light travels from air to a material with some refractive index and is reflected from the top and bottom surfaces. Assuming the medium below the wedge is the same as that above, i.e. air, there must be one π phase change, and this is due to reflection off the top or bottom surface depending on whether the material or air has the higher refractive index. Therefore, the conditions are:
constructive interference - 2nαx = (p + 1/2 )λ
destructive interference - 2nαx = p λ,
What is single finite width slit diffraction?
- single slit of width (a) = very large number N of equally spaced narrow slits (d=separation of slits) i.e. Nd=a (as N→infinity, d or a/N→0)
What is intensity for single slit diffraction? What happens when x=(π/λ)asinθ and x→0? Hence when is intensity max. and min?
- replace d with a/N in intensity of an array of N slits (diffraction grating)
- use small angle approximation for denominator => get factor of N2
- but as N→infinity => amount of light transmitted from each region shrinks by 1/N hence effective amplitude should be divided by N to reflect this (since intensity is proportional to amplitude squared - divide by N2)
- I→I0 as x→0
- min. when (π/λ)asinθ=mπ
- max. when π/λ)asinθ=(m+0.5)π
What is the limit of resolution for human eye?
- using θr=1.22λ/D
What is the intensity for finite width slit? What does it mean when d>a? And what is primary max. for diffraction grating and min. for finite single slit? What does this mean? What makes a good grating? And why?
- Product of that for grating & single slit
- d>a => 1st min. of single slit at greater angle than 1st primary max. of diffracton grating away from centre
- primary max. of diffraction grating decreases until 1st single slit min. then rise and fall again but at smaller peaks
- primary max. of diffraction grating when dsinθ=mλ
- min. of single slit when asinθ=kλ
- hence when d/a=m/k => coincide so order m grating maxima missing
- good gratings when d>>a since slower fall of primary max.
What is the eqn for a general periodic wave?
