11.5

Question 1

F(t) has a limit at c if and only if

Answer 1

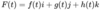
f, g, and h have limits at c.

Question 2

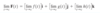
Let F and G be differentiable, vector-valued functions, p a differentiable, real-valued function, and c a scalar. Then:

D_t[F(t) + G(t)]

Answer 2

F’(t) + G’(t)

Question 3

Let F and G be differentiable, vector-valued functions, p a differentiable, real-valued function, and c a scalar. Then:

D_t[cF(t)]

Answer 3

cF’(t)

Question 4

Let F and G be differentiable, vector-valued functions, p a differentiable, real-valued function, and c a scalar. Then:

D_t[p(t)F(t)]

Answer 4

p(t)F’(t) + p’(t)F(t)

Question 5

Let F and G be differentiable, vector-valued functions, p a differentiable, real-valued function, and c a scalar. Then:

D_t[F(t) \cdot aG(t)]

Answer 5

F(t) \cdot G’(t) + G(t) \cdot F’(t)

Question 6

Let F and G be differentiable, vector-valued functions, p a differentiable, real-valued function, and c a scalar. Then:

D_t[F(t) x G(t)]

Answer 6

F(t) x G’(t) + F’(t) x G(t)

Question 7

Let F and G be differentiable, vector-valued functions, p a differentiable, real-valued function, and c a scalar. Then:

D_t[F(p(t))]

Answer 7

F’(p(t))p’(t) (chain rule)