11 - Strings and Text 2

Question 1

How can a suffix tree for a string S be derived from a suffix trie?

Answer 1

• collapse each path consisting of unary branch nodes into a single edge
• label each new edge with concatentation of labels from the corresponding trie edges

Question 2

Suffix tree of a string S

Answer 2

• construct S* from S by appending a character ($) that doesn’t appear in S
• suffix tree of S* (loosely, of S) is a rooted tree in which
  
  • each edge labelled by a string (its edge label)
  • all branch nodes have >= 2 children
  • no 2 children of a node have edge labels beginning with same character
  • 1-to-1 corrsespondence between suffixes of S* and leaf nodes v, in sense that the path label of v is precisely that suffix
    
    • the path label of a node is concatenation of edge labels on path from root to that node

Question 3

What are the properties of a suffix tree?

Answer 3

• Number of leaf nodes is n+1 (n = |S|)
• number of branch nodes is <= n
• total number of nodes is O(n)
• sum of lengths of edge labels is same as suffix trie
  
  • no better than O(n²)

Question 4

How to avoid space overhead in suffix tree?

Answer 4

• Use short edge labels
  
  • replace a string X by pair of integers (i, j) such that
    
    • X = S*(i .. j)
    • each short edge label has length O(1)
    • so sum of lengths of edge labels is O(n)

Question 5

Example

Answer 5

Question 6

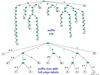
Example

suffix tree with full edge labels vs short edge labels

Answer 6

Question 7

What is naive method for constructing a suffix tree

Answer 7

• Let S be string of length n. Append a character to form S*
• Creating suffix tree T:
  
  • 1) create suffix trie for S*
    
    • SuffTrie suffTrie = new SuffTrie();
    • for (int j=1; j <= n+1; j++)
    • insert(suffTrie, s[j … n+1);
  • 2) amalgamate edges of paths containing unary branch nodes into single edges
  • 3) create short edge labels
• Worst case complexity
  
  • 1) O(n²)
  • 2) O(n²)
  • 3) O(n²)
• Overall: O(n²)
• Space complexity O(n²)
  *

Question 8

What is the better method for constructing a suffix tree T?

Answer 8

• Create suffix tree (with short labels) for S* directly:
  
  • SuffTree suffTree = new SuffTree();
  • for (int j=1; j<=n+1; j++)
  • insert(suffTree, s[j .. n+1]);
• To insert a suffix, follow an existing path and split from a certain point
• Worst case time complexity still O(n²)
• But space complexity O(n)
• Average time complexity O(n log n)

Question 9

Example

comes after better method for constructing suffix tree

Answer 9

Question 10

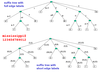
Searching a text T of length n, for a string S of length m in a suffix tree?

Answer 10

• build suffix tree for T
  
  • O(n) time
• follow a path from root matching characters
  
  • O(m) time
• all occurrences are represented by leaf node descendants from point where search ends
• can search text of length n for k short strings of total r in O(n + r) time
• e.g. find all occurences of is in mississippi

Question 11

Example of finding occurences in suffix tree

Answer 11

Question 12

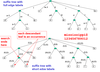
Finding longest repeated substring in text T, length n

Answer 12

• build suffix tree for T
  
  • O(n) time
• traverse the tree
• a longest repeat is represented by a branch node having greatest string depth
  
  • string depth of a node is sum of lengths of the edge labels on the path from root to that node
  • i.e. it is length of the path label of that node
• traversal is also O(n) is overall O(n)

Question 13

Example of finding longest repeated substring in suffix tree

Answer 13

Question 14

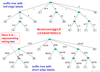
Finding longest common substring (LCSt) of strings S₁, S₂ of lengths m, n in suffix tree

Answer 14

• e.g. S1 = dadbcdb and S2 = abcdacda
• build generalised suffix tree T for S₁ and S₂
• this is the suffix tree for S = S₁ # S₂
  
  • i.e. $ is the concatentation of S₁, #, S₂, $ in that order (where # nor $ occurs in S₁ or S₂)
• traverse tree
  
  • longest common substring is represented by a common branch node with greatest string depth
• a branch node is common if it has 2 descendant leaf nodes representing positions starting in S₁ and S₂

Question 15

Example of finding longest common substring 1/2

Answer 15

Question 16

Example of finding longest common substring 2/2

Answer 16

Question 17

Identifying common branch nodes

Answer 17

* maintain booleans at each node v of T as follows:

* define b<sub>i</sub>(v) as true if and only if
    * path label of a descendant leaf node of v starts in string S<sub>i</sub> ∈ (i {1, 2})
* a branch node v of T is common if and only if b<sub>1</sub>(v) ∧ b<sub>2</sub>(v)

• computing the b_i values
  
  • let v be a leaf node corresponding to suffix no. j of S, so path label of v is S(j .. m+n+2)
  • b₁(v) = true if and only if 1 <= j <= m
  • b₂(v) = true if and only if m+2 <= j <= m+n+1
  • for a branch node v, b_i(v) = b_i(w₁) ∨ b_i(w₂) ∨ … ∨ b_i(w_r)
    
    • where w₁, …, w_r are the children of v (i {1,2})

Question 18

Overall of finding longest common substring problem (LCSt)

Answer 18

• Given strings S₁, S₂ of lengths m, n

1. build generalised suffix tree T
   
   • O(m+n) time
2. calculate b_i(v) values
   
   • O(m+n) time using a traversal of T
3. output path label of a common branch node w of T with max string depth
   
   • O(m+n) time

• in practise, w may be computed during travesal in 2
• overall O(m+n) time and space

Question 19

Example of finding longest common substring with questions

Answer 19