(11) Sampling and Estimation Flashcards
LOS 11. a: Define simple random sampling and a sampling distribution.
Simple random sampling is a method of selecting a sample in a way that each item or person in the population being studied has the same probability of being included in the sample.
LOS 11. a: Define simple random sampling and a sampling distribution.
A sampling distribution is the distribution of all values that a sample statistic can take on when computed from samples of identical size randomly drawn from the same population.
LOS 11. b: Explain sampling error.
Sampling error is the difference between a sample statistic and its corresponding population parameter (e.g., the sample mean minus the population mean).
LOS 11. c: Distinguish between simple random and stratified random sampling.
Stratified random sampling involves randomly selecting samples proportionally from subgroups that are formed based on one or more distinguishing characteristics, so that the sample will have the same distribution of these characteristics as the overall population.
LOS 11. d: Distinguish between time-series and cross-sectional data.
Time-series data consists of observations taken at specific and equally spaced points in time.
Cross-sectional data consists of observations taken at a single point in time.
LOS 11. e: Explain the central limit theorem and its importance.
The central limit theorem states that for a population with a mean µ and a finite variance σ2, the sampling distribution of the sample mean for all possible samples of size n (for n >= 30) will be approximately normally distributed with a mean equal to µ and a variance equal to σ2/n.
LOS 11. f: Calculate and interpret the standard error of the sample mean.
The standard error of the sample mean is the standard deviation of the distribution of the sample means and is calculated as σXbar = s/(n1/2), where σ, the population standard deviation, is known, and the sx = s/(n1/2), where s, the sample standard deviation, is used because the population standard deviation is unknown.
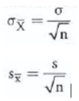
LOS 11. g: Identify and describe desirable properties of an estimator.
Desirable statistic properties of an estimator include unbiasedness (sign of estimation error is random), efficiency (lower sampling error than any other unbiased estimator), and consistency (variance of sampling error decreases with sample size).
LOS 11. h: Distinguish between a point estimate and a confidence interval estimate of a population parameter.
Point estimates are single value estimates of population parameters. An estimator is a formula used to compute a point estimate.
LOS 11. h: Distinguish between a point estimate and a confidence interval estimate of a population parameter.
Confidence intervals are ranges of values, within which the actual value of the parameter will lie with a given probability.
LOS 11. h: Distinguish between a point estimate and a confidence interval estimate of a population parameter. The reliability factor.
The reliability factor is a number that depends on the sampling distribution of the point estimate and the probability that the point estimate falls on the confidence interval.
LOS 11. i: Describe properties of Student’s t-distribution and calculate and interpret its degrees of freedom.
The t-distribution is similar, but not identical, to the normal distribution in shape-it is defined by the degrees of freedom and has fatter tails compared to the normal distribution.
Degrees of freedom for the t-distirbution are equal to n-1. Student’s t-distribution is closer to the normal distribution when df is greater, and confidence intervals are narrower when df is greater.
LOS 11. j: Calculate and interpret a confidence interval for a population mean, given a normal distribution with 1) a known population variance, 2) an unknown population variance, or 3) an unknown variance and a large sample size.
For a normally distributed population, a confidence interval for its mean can be constructed using a z-statistic when variance is known, and a t-statistic whne the variance is unknown. The z-statistic is acceptable in the case of a normal population with an unknown variance if the sample size is large (30+).
LOS 11. j: Calculate and interpret a confidence interval for a population mean, given a normal distribution with 1) a known population variance, 2) an unknown population variance, or 3) an unknown variance and a large sample size. Chart.
LOS 11. k: Describe the issues regarding selection of the appropriate sample size, data-mining bias, sample selection bias, survivorship bias, look-ahead bias, and time-period bias.
Increasing the sample size will generally improve parameter estimates and narrow confidence intervals. The cost of more data must be weighted against these benefits, and adding data that is not generated by the same distribution will not necessarily improve accuracy or narrow confidence intervals.
